Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 14.Problemas - Ex. 36
Considere a combustão de gás hidrogênio em uma mistura de hidrogênio e oxigênio adjacente à parede metálica de uma câmara de combustão. A combustão ocorre a temperatura e pressão constantes, de acordo com a reação química . Medições efetuadas sob condições de regime estacionário a uma distância de da parede indicam que as concentrações molares de hidrogênio, de oxigênio e de vapor de água são e , respectivamente. A taxa de geração de vapor de água é de ao longo de toda a região de interesse. O coeficiente de difusão binária de cada espécie nas demais espécies é igual a .
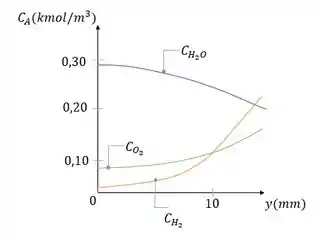
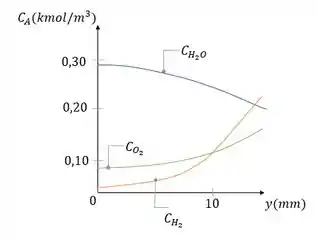
(a) Determine uma expressão e faça um gráfico qualitativo de como uma função da distância da parede.
(b) Determine o valor de na parede.
(c) Nas mesmas coordenadas usadas na parte (a), esboce curvas para as concentrações de oxigênio e de vapor de água.
(d) Qual é o fluxo molar de vapor de água em ?
Passo 1
Nessa questão nós temos uma combustão a temperatura e pressão constantes de uma mistura hidrogênio-oxigênio adjacente a uma parede de metal de acordo com a reação,
As concentrações molares de hidrogênio, oxigênio e vapor de água são e , respectivamente. A taxa de geração de vapor de água é de .
Com essas informações vamos encontrar a expressão para em função da distância da parede e fazer a plotagem qualitativa. Além de encontrar também na parede, fazer o esboço também das curvas para e e o fluxo molar de água em .
Passo 2
Para resolver essa questão vamos assumir:
(1) Condições de estado estacionário;
(2) Difusão unidimensional;
(3) Meio estacionário;
(4) Propriedades constantes, incluindo pressão e temperatura.
A equação de conservação de espécies e sua solução geral são,
A condição de contorno na parede deve ser,
De modo que .
Passo 3
Para a espécie hidrogênio, avaliamos sabendo que
E,
De acordo com a reação química. Então,
Portanto, a distribuição da concentração de espécies de hidrogênio é,
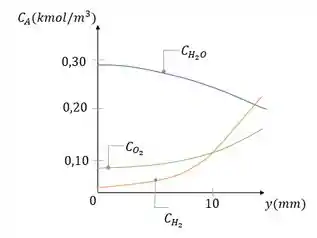
Que é parabólico com inclinação zero na parede.
Passo 4
O valor de na parede é,
Passo 5
A distribuição da concentração de espécies de vapor de água será da mesma forma,
Com para a condição da parede, encontramos em ,
Então, na parede é,
E sua distribuição aparece no gráfico do passo anterior. Sabendo que,
Pela mesma análise, encontramos,
E sua forma, também parabólica com inclinação zero na parede, é mostrada no gráfico.
Passo 6
O fluxo molar do vapor de água em é dado pela lei de Fick,
E usando a distribuição de concentração encontramos,
E avaliando no local , o fluxo de espécies é,
Resposta
