Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 11.Problemas - Ex. 6
Um projeto inovador para um condensador consiste em um tubo com condutividade térmica de 200 W/(m · K) com aletas longitudinais firmemente encaixadas no interior de um tubo maior. Um refrigerante, em condensação a 45 °C, escoa axialmente através do tubo interno, enquanto água, a uma vazão de 0,012 kg/s, escoa pelos seis canais formados ao redor do tubo interno. Os diâmetros pertinentes são = 10 mm, = 14 mm e = 50 mm, enquanto a espessura das aletas é t = 2 mm. Considere que o coeficiente de transferência de calor associado ao refrigerante em condensação seja extremamente elevado.
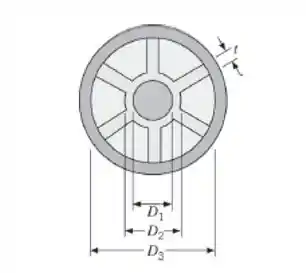
Determine a taxa de remoção de calor por unidade de comprimento do tubo em uma seção do tubo na qual a água está a 15 °C.
Passo 1
Antes de começar, vamos dar um pulo lá no apêndice A na tabela A.6 para pegar as propriedades da água que escoa através dos canais ao redor do tubo interno a 15 °C = 288 K, então, para essa temperatura, temos:
Tá legal! Queremos encontrar a taxa de transferência e calor do gás para a água por unidade de comprimento do tubo, então, utilizando o coeficiente global de transferência de calor da parte fria, podemos escrever a taxa de transferência de calor através da equação de resfriamento de Newton da seguinte forma:
E, por unidade de comprimento, teremos:
Então, já tendo as temperaturas do lado quente e frio, precisamos encontrar o valor da expressão . Dessa forma, através da equação 11.1b, temos a seguinte relação:
Então, sendo a resistência da parede, dada pela equação 3.33 vista lá no capítulo 3, que nesse caso é a resistência de condução e como o enunciado nos disse que o coeficiente de transferência de calor associado ao refrigerante é muito alto, isso quer dizer que podemos desprezar o terceiro termo da equação acima. Então, com isso, a equação acima se torna:
Então, como estamos interessados na relação por unidade de comprimento, podemos dividir os dois lados por , dessa forma, teremos:
Passo 2
Então, precisamos calcular as expressões para a área fria, o coeficiente convectivo da parte fria e a eficiência da superfície fria . Começando então pelo coeficiente convectivo da parte fria, precisamos primeiro calcular o diâmetro hidráulico da seção que é dado por:
Em que é a área transversal da passagem e é o perímetro. Então, a área transversal será dada pela área total menos a área das 6 aletas dividido pelo número total de seções, então teremos:
Substituindo os valores conhecidos, teremos:
Agora, para o perímetro de uma seção, teremos:
Substituindo os valores conhecidos, teremos:
Então o diâmetro hidráulico da parte fria será:
Passo 3
Com o valor do diâmetro hidráulico podemos calcular o número de Reynolds, dado por:
No entanto, temos a informação da vazão mássica, que por sua vez é dada por:
Isolando a densidade dessa expressão, teremos:
E, substituindo essa expressão na equação para Reynolds, chegamos em:
E, substituindo os valores conhecidos, lembrando que estamos calculando o valor por seção, chegaremos em:
Então como temos Reynolds menor que 2300, o escoamento será laminar. Então, assumindo que o escoamento é totalmente desenvolvido, teremos um Nusselt de:
Sabendo que o Nusselt se relaciona com o coeficiente convectivo através da seguinte equação:
Substituindo os valores conhecidos, chegamos em:
Passo 4
Agora, a eficiência da superfície fria será dada pela equação 11.3, onde temos:
Em que representa a área das aletas, a área superficial total e a sua eficiência. Vamos começar calculando a área das aletas. Sabendo que temos aletas retangulares, e calculando por unidade de comprimento, teremos:
Agora, a área externa, ou área fria , por unidade de comprimento, será então dada pela área das aletas mais a superfície externa original total subtraída das espessuras das aletas, ou seja:
Agora vamos calcular a eficiência das aletas. Então supondo extremidade adiabática, podemos utilizar a equação 11.4 para a eficiência, onde temos:
Em que será dado por:
Então, substituindo os valores conhecidos na equação para , temos:
E, sabendo que o comprimento das aletas (altura) é dada pela diferença entre os raios do tubo maior isolado e do raio externo do tubo menor, teremos:
Então, substituindo os valores conhecidos na equação para a eficiência das aletas, temos:
Agora, substituindo esse valor para a eficiência da superfície fria, teremos:
Passo 5
Agora, retornando à equação escrita lá no passo 1 para e substituindo os valores conhecidos, teremos:
Então, finalmente, substituindo essa expressão na equação para a taxa de transferência de calor lá do passo 1, temos: