Um recuperador é um trocador de calor que aquece o ar usado em um processo de combustão pela extração de energia dos produtos de combustão (o gás de exaustão). Considere a utilização de um trocador de calor com escoamentos cruzados e um único passe como recuperador.

Oitenta tubos cerâmicos de carbeto de silício , com diâmetros interno e externo iguais a e , respectivamente, e com comprimento , são posicionados formando uma matriz de tubos alinhados com passos longitudinal e transversal de e , respectivamente. Ar frio escoa transversalmente sobre a matriz de tubos (escoamento cruzado) com condições a montante que equivalem a e , enquanto os gases quentes de exaustão, com temperatura de alimentação de , passam pelo interior dos tubos. As superfícies externas dos tubos estão limpas, enquanto as superfícies internas são caracterizadas por um fator de deposição de . As vazões do ar e dos gases de exaustão são de e , respectivamente. Como primeiras aproximações, (1) estime todas as propriedades necessárias do ar a e , (2) suponha que os gases de exaustão tenham as propriedades do ar a e , e (3) admita que a temperatura na parede do tubo esteja a com o propósito de levar em consideração o efeito de propriedades variáveis na transferência de calor por convecção.
(a) Se existir uma economia de combustível da ordem de associada a cada aumento de na temperatura do ar de combustão acima de , qual é a economia percentual de combustível para as condições especificadas?
(b) O desempenho do recuperador é fortemente influenciado pelo produto do coeficiente global de transferência de calor e da área total, . Calcule e represente graficamente e a economia percentual de combustível como funções do valor de para . Sem alterar as vazões, quais são as medidas que podem ser tomadas para aumentar o valor de ?
Passo 1
Vamos lá!! Nosso problema se trata de um sistema não muito complexo de trocador de calor tendo isso em mente vamos ilustrar isso com nosso esqueminha pra facilitar o entendimento do problema.
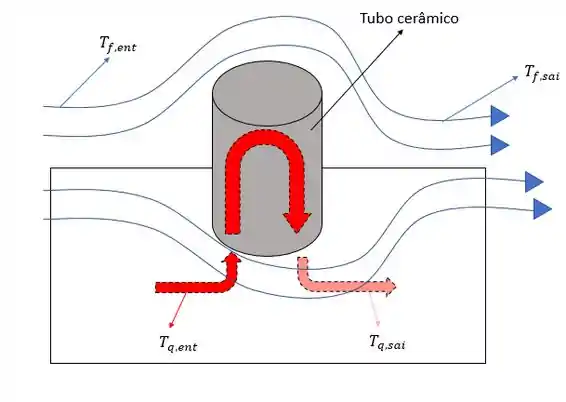
Agora precisamos fazer nossas famosas considerações. Hehe (u.u)
Passo 2
(a)
Vamos lá! Vamos usar os da tabela e para ar a e a , vamos começar calculando nosso coeficiente calorifico, assim temos:
Sendo e , temos que do escoamento para um único tubo temos:
Onde é o número de tubos:
Considerando que o escoamento é completamente desenvolvido, usando a relação de temos:
Agora precisamos calcular o coeficiente convectivo para parte externa do tubo cerâmico:
Para o escoamento na região externa temos:
Da relação de :
Agora finalmente calculando o coeficiente médio convectivo na superfície temos:
Calculando nosso coeficiente convectivo global temos:
Passo 3
(a) continuação
Agora pra matar essa galera!
Vamos calcular nossa economia, mas antes vamos fazer uma análise das taxas de calor para esse sistema:
Da figura , da equação
Assim temos que o calor é:
A temperatura de saída é dada por:
Assim nossa economia é dada por:
Passo 4
(b)
Aumentando o coeficiente convectivo global vamos aumentar a taxa de transferência de calor assim aumentando a temperatura de saída e aumentando nossa economia, refazendo o passo e variando temos um arranjo, montando isso em forma de gráfico temos:
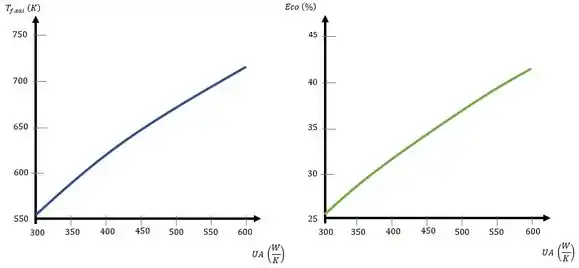
Terminamos mais essa galera!
Resposta
(a)
(b) Gráfico vide passo a passo