Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 11.Problemas - Ex. 58

Um trocador de calor casco e tubos, com um passe no casco e 20 passes nos tubos, utiliza água quente no lado dos tubos para aquecer óleo que escoa pelo lado do casco. O único tubo, de cobre, tem diâmetros interno e externo de 20 e 24   m m , e um comprimento por passe de 3   m . A água entra a 87 ° C e 0,2   k g / s , e sai a 27 ° C . As temperaturas de entrada e de saída do óleo são 7 e 37 ° C . Qual é o valor do coeficiente de transferência de calor por convecção médio na superfície externa do tubo?

Passo 1

Vamos lá!! Nosso problema se trata de um sistema simples de trocador de calor tendo isso em mente vamos ilustrar isso com nosso esqueminha pra facilitar o entendimento do problema.

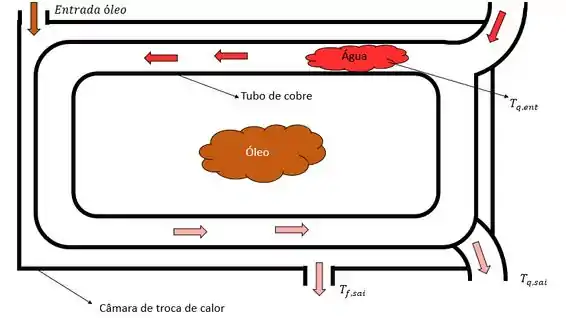
Agora precisamos fazer nossas famosas considerações. Hehe (u.u)

I - P r o p r i e d a d e s   c o n s t a n t e s

I I - R e g i m e   p e r m a n e n t e

I I I - T r o c a   d e   c a l o r   c o m   a   v i z i n h a n ç a   d e s p r e z í v e l

I V - T i p o   d e   ó l e o   n ã o   e s p e c i f i c a d o

V - N ã o   h á   c o n s t r i ç ã o   d o   f l u x o

V I - R e s i s t ê n c i a   t e r m i c a   n a   p a r e d e   d o   t u b o   é   d e s p r e z í v e l

Passo 2

(a)

Vamos lá! Vamos usar os da tabela A - 6 e para água a 285   K , vamos começar calculando o coeficiente de calor para a água, mas antes temos que avaliar o seu escoamento, assim temos:

R e = ρ u m D μ = 4 m ˙ μ ⋅ D π

R e = 26.038

Temos que o escoamento é turbulento, usando a relação de D i t t u s - B o e l t e r temos:

h = N u ⋅ k D = k D ⋅ 0,023 R e 4 5 ⋅ P r 0,3

h = 3594 W m 2 ⋅ K

Calculando o coeficiente calorifico temos:

C q = m ˙ q c p , q = 8 36,8   W K

q = C q T q ,   e n t - T q ,   s a i = 50.208   W

C f = q T f ,   e n t - T f ,   s a i = 1674   W K

C r = C m i n C m a x = 0,5

Calculando a eficiência:

q m a x = C m i n T q ,   e n t - T f ,   e n t = 66.944   W

ε = q q m a x = 0,75

Das equações 11.30 temos:

E = 2 ε - 1 + C r 1 + C r 2 1 2 = 1,04

N T U = - 1 + C r 2 ⋅ ln ⁡ E - 1 E + 1 = 3,44

Assim temos que o produto da área pelo coeficiente convectivo global é:

U A = C m i n ⋅ N T U = 2881   W K

Agora finalmente calculando o coeficiente médio convectivo na superfície temos:

h - = 1 D e x t ⋅ 1 U A - 1 ⋅ N t π L ⋅ 1 h D i n t - 1

Onde N t é o número de tubos, assim:

h - = 808   W m 2 ⋅ K

Terminamos mais essa galera!

Resposta

h - = 808   W m 2 ⋅ K

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

79 – Como o N T U de um trocador de calor é definido? O que isso representa? Um trocador de calor com grande N T U (digamos, 10) é necessariamente bom trocador?
76 - Considere um trocador de calor de tubo duplo em contracorrente. A fim deaumentar a transferência de calor, o comprimento do trocador de calor agora é dobrado.Você acha que sua efetividade também
80 - Considere um trocador de calor que tem NTU 4. Alguém propõe dobrar o tamanho do trocador de calor e, assim, dobrar o NTU para 8, a fim de aumentar a efetividade do trocador de calor e, assim, eco
74 - Explique como a taxa máxima de transferência de calor possível Q ˙ m a x em um trocador de calor pode ser determinada quando as vazões mássicas, os calores específicos e as temperaturas de entrad
82 – Um trocador de calor de fluxo cruzado com ambos os fluidos não misturados tem coeficiente global de transferência de calor 200 W m 2 ⋅ K e área de superfície de transferência de calor de 400m 2 .