Em um supercomputador, os atrasos na propagação de sinais são reduzidos utilizando-se configurações com circuitos de alta densidade, que são resfriados por sua imersão em um líquido dielétrico especial. O fluido é bombeado em um circuito fechado através do computador e de um trocador de calor casco e tubos adjacentes, que tem um passe no casco e dois nos tubos.
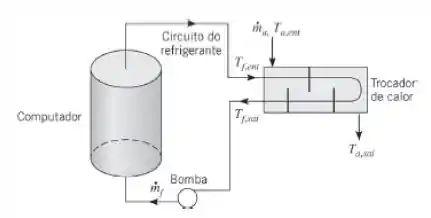
Durante a operação em condições normais, o calor gerado no interior do computador é transferido para o fluido dielétrico que passa através do computador a uma vazão de . Por sua vez, o fluido passa através dos tubos do trocador de calor e o calor é transferido para a água que passa pelo lado externo dos tubos. Pode ser considerado que o fluido dielétrico tem propriedades constantes iguais a: e . Durante a operação em condições normais, água gelada, a uma vazão de e uma temperatura de entrada de , escoa sobre os tubos. A água tem um calor específico de e proporciona um coeficiente convectivo médio de na superfície externa dos tubos.
(a) Se o trocador de calor tem tubos com paredes delgadas, cada um com de diâmetro, e admite-se a existência de escoamento plenamente desenvolvido no interior dos tubos, qual é o coeficiente de transferência de calor associado ao escoamento no interior dos tubos?
(b) Se o fluido dielétrico entra no trocador de calor a e deve deixá-lo a , qual deve ser o comprimento dos tubos por passe?
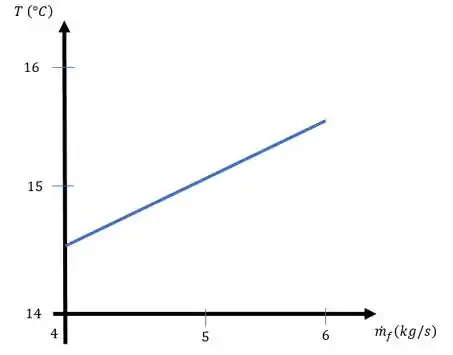
(c) Para o trocador de calor com o comprimento de tubo por passe determinado na parte (b), represente graficamente a temperatura de saída do fluido dielétrico como uma função de sua vazão para . Leve em consideração as variações correspondentes no coeficiente global de transferência de calor, porém suponha que todas as demais condições permaneçam sem alteração.
(d) O responsável local pela instalação do computador está preocupado com variações no desempenho do refrigerador, que fornece a água gelada , e os seus efeitos sobre a temperatura de saída do fluido dielétrico. Com todas as demais condições permanecendo sem alteração, determine o efeito de uma variação de na vazão mássica da água fria sobre o valor de .
(e) Repita a análise de desempenho da parte (d) para determinar o efeito de uma variação de na temperatura de entrada da água sobre , com todas as demais condições permanecendo inalteradas.
Passo 1
Vamos lá!!
O problema pra entendermos melhor nosso problema precisamos entender o conceito refrigeração, tá na parte de teoria da termodinâmica, nós temos aqui no site então dá uma olhada rapidinho.
Agora podemos seguir com nossa questão,
Mas agora vamos ilustrar isso com nosso esqueminha pra facilitar.
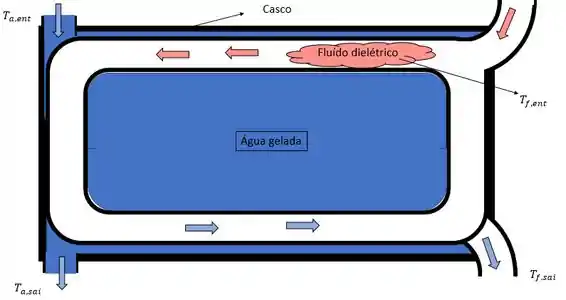
Sendo o nosso tubo está enrolado e tem duas voltas.
Agora precisamos fazer nossas famosas considerações. Hehe (u.u)
Passo 2
(a)
Vamos lá! os dados são entregues pelo nosso problema então não precisamos consultar as tabelas no final do livro \o/.
Vamos avaliar o escoamento para um único tubo, calculando nosso número de Reynolds temos:
Agora vamos calcular nosso coeficiente convectivo usando a relação de temos:
Passo 3
(b)
Agora vamos calcular nosso coeficiente calorifico, assim temos:
Sendo e , temos que
Da relação da eficiência temos:
Com nossa eficiência podemos olhar na figura para descobrirmos que nosso coeficiente .
fazendo uma relação conseguimos encontrar o comprimento do tubo para uma volta.
Onde:
Sendo a área total dos tubos com duas voltas, dada por:
Isolando e substituindo na formula do coeficiente temos:
Substituindo para encontrarmos o comprimento de uma volta do tubo:
Passo 4
(c)
Se refazermos o passo com o comprimento do tubo constante, variando a vazão do fluído dielétrico no intervalo apresentado, vamos encontrar um arranjo de temperatura de saída, vamos montar isso em forma de gráfico.
Mas para entendermos o processo vamos alterar a equação e sem alterarmos a eficiência:
Com constante, assim temos:
P.S: podemos resolver isso com um software de sua preferência, normalmente uso um laço de repetição e uso a função plot para mostrar os resultados.
Passo 5
(d)
Do coeficiente calorifico temos que para uma variação de na vazão da água gelada com as demais propriedades constantes:
Como tem que ser constante para uma variação em temos que variar
Sendo .
Que por consequência da relação da eficiência temos:
Assim como nossa eficiência tem que ser constante com valor.
Assim variando de temos:
Substituindo tudo chegamos a uma variação de:
Passo 6
(e)
da relação da eficiência temos:
Como se variarmos de forma:
Organizando a equação temos que:
Substituindo os valores:
Isso é tudo pessoal!

Resposta
(a)
(b)
(c) gráfico vide passo a passo
(d)
(e)