A taxa de combustão de massa de um gás inflamável é uma função da espessura da chama, , da massa específica do gás, , da difusividade térmica,, e da difusividade de massa . Usando a análise dimensional, determine a forma funcional desta dependência em função dos parâmetros adimensionais. Note que e possuem as dimensões .
Passo 1
Nessa questão nós temos a relação funcional entre a taxa de queima em massa de uma mistura combustível e outros parâmetros físicos e queremos encontrar a dependência da taxa de queima em massa.
Passo 2
Usando o procedimento de Buckingham temos que o número de parâmetros é:
![]()
Selecionando as dimensões primárias
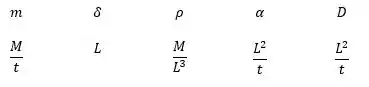
E os parâmetros repetidos:
![]()
Passo 3
Então nós temos grupos sem dimensão. Configurando as seguintes equações dimensionais:
Somando os expoentes:
Temos que a solução do sistema é:
Então:
Passo 4
Para o segundo grupo temos:
Somando os expoentes:
Temos que a solução do sistema é:
Então:
Passo 5
Verificando usando como dimensões primárias temos:
A relação funcional é: