Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 194

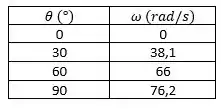
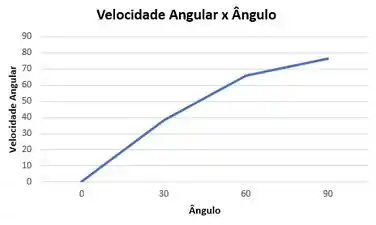
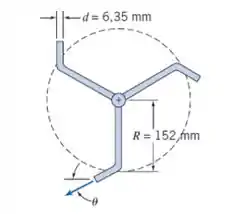
O regador de gramados mostrado é suprido com água a uma taxa de 68   L / m i n . Desprezando o atrito no pivô, determine a velocidade angular do regador em regime permanente para θ = 30 ° . Trace um gráfico da velocidade angular do regador em regime permanente para 0 ≤ θ ≤ 90 ° .

Passo 1

Equação:

r × F s + ∫ V C r × g ρ d ∀ + T e i x o - ∫ V C r × 2 ω × V + ω × ω × r + ω × r ρ d ∀ = ∂ ∂ t ∫ V C r × V ρ d ∀ + ∫ S C r × V   ρ V d A

Considerações Iniciais:

  1. Fluxo Constante;
  2. Escoamento Estacionário;
  3. Cancelamento do torque no corpo;
  4. F S = 0 ;
  5. Não há k ^ na aceleração centrípeta;
  6. T e i x o = 0 .

Passo 2

Realizando as considerações:

- ∫ V C r × 2 ω × V ρ d ∀ = ∫ S C r × V   ρ V d A

Analisando um eixo do regador.

Temos para a primeira parte da equação:

- ∫ V C r × 2 ω × V ρ d ∀ = - ∫ V C 2 ω V r ρ D ∀ = - ∫ 0 R 2 ω V r ρ A D r = - ω V R 2 ρ A  

Sendo V A = Q 3 :

- ∫ V C r × 2 ω × V ρ d ∀ = - ω R 2 ρ Q 3  

Para a segunda parte da equação:

∫ S C r × V   ρ V d A = R î × - V   s e n   θ j ^ V ρ A = - R ρ V 2 A   s e n   θ

Sendo V A = Q 3 :

∫ S C r × V   ρ V d A = - ρ R Q V 3 s e n   θ  

Assim, a equação inicial fica:

- ω R 2 ρ Q 3 = - ρ R Q V 3 s e n   θ  

Isolando ω :

ω = V R s e n   θ

Passo 3

Sendo:

V = Q 3 A = 4 Q 3 π d 2 ;

R = 152   m m = 0,152   m ;

D = 6,35   m m = 0,00635   m ;

Q = 0,0011   m 3 / s .

Temos:

ω = V R s e n   θ = 4 Q 6 π R d 2 s e n   θ = 4 ⋅ 0,0011 3 ⋅ π ⋅ 0,152 ⋅ 0,00635 2 s e n   θ = 76,2   s e n   θ

Para θ = 30 ° , temos:

ω = 76,2   s e n   30 ° = 38,1   r a d / s

Passo 4

Traçando o Gráfico:

Resposta

ω = 38,1   r a d / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Escreva a equação do momento do escoamento unidimensional estacionário para o caso de ausência de força externa e explique o significado físico de seus termos.
Qual a importância do fator de correção do fluxo do momento na análise do momento dos sistemas de escoamento? Para qual tipo de escoamento ele é significativo e deve ser considerando na análise: escoa
Explique a importância do teorema de transporte de Reynolds na mecânica dos fluidos e descreva como a equação do momento linear é obtida a partir dele.
Enuncie a primeira, segunda e terceira leis de Newton.
Um foguete no espaço (nenhum atrito ou resistência ao movimento) pode expelir gases a uma certa velocidade alta V em relação a si mesmo. V é o limite superior para velocidade final do foguete?