Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 5.Problemas - Ex. 47

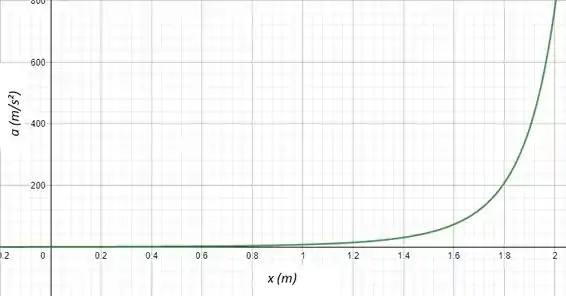
5.47 Um líquido incompressível com viscosidade desprezível escoa através de um tubo horizontal. O escoamento é permanente. O diâmetro do tubo varia linearmente de 10   c m até 2,5   c m ao longo de um comprimento de 2   m . Desenvolva uma expressão para a aceleração de uma partícula fluida ao longo da linha central do tubo. Trace um gráfico da velocidade e da aceleração na linha central v e r s u s a posição ao longo do tubo, se a velocidade na linha central foi igual a 1   m / s .

Passo 1

Vamos começar considerando fluido incompressível e fluxo uniforme na entrada e na saída.

Sabemos que a área por de representada por:

A = π D 2 4

Mas como o diamentro varia linearmente, podemos achar uma expressão para o diâmetro variando com x: (equação de uma reta)

D = a x + b

Mas temos o diâmetro de entrada: (em x = 0 )

D = D e

D e = a 0 + b

b = D e

E temos o diâmetro de saída: (em x = L )

D = D s

D s = a L + D e

a = D s - D e L

Então:

D =   D s - D e L x + D e

Passo 2

Pela equação da continuidade temos:

V e A e = V A

V e π D e 2 4 = V π D 2 4

V e π D e 2 4 = V π D s - D e L x + D e 2 4

V = V e D e 2 D s - D e L x + D e 2

V = 1 0,1 2 0,025 - 0,1 2 x + 0,1 2

V = 0,01 - 0,0375 x + 0,1 2

Passo 3

Como só tem variação em x, então a aceleração é dada por:

a p x = V ∂ V ∂ x

Calculando a derivada parcial:

∂ V ∂ x = D s - D e L - 2 V e D e 2 D s - D e L x + D e 3

∂ V ∂ x = - 2 V e D e 2 D s - D e L D s - D e L x + D e 3

Então:

a p x = V e D e 2 D s - D e L x + D e 2 - 2 V e D e 2 D s - D e L D s - D e L x + D e 3

a p x = - 2 V e 2 D e 4 D s - D e L D s - D e L x + D e 5

Como consideramos fluxo uniforme podemos considerar V e a velocidade na linha central. ( V e = 1   m / s )

a p x = - 2 1 2 0,1 4 ( 0,025 ) - 0,1 2 0,025 - 0,1 2 x + 0,1 5

a p x = 7,5 × 10 - 6 - 0,0375 x + 0,1 5

Resposta

a p x = - 2 V e 2 D e 4 D s - D e L D s - D e L x + D e 5

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5.79 Considere o campo de escoamento representado pela função de corrente ψ = - A / 2 x 2 + y 2 , em que A é constante. Esse é um possível escoamento bidimensional incompressível? O escoamento é irrot
5.78 Considere um campo de velocidade para um movimento paralelo ao eixo x com cisalhamento constante. A taxa de cisalhamento é du/dy=A, em que A = 0,1s - 1 . Obtenha uma expressão para o campo de vel
5.77 Considere o campo de escoamento representado pela função de corrente ψ = x 6 - 15 x 4 y 2 + 15 x 2 y 4 - y 6 . Esse é um possível escoamento bidimensional incompressível? O escoamento é irrotacio
5.80 Considere o campo de escoamento representado pela função de corrente ψ = A x y + A y 2 , em que A = 1s - 1 . Mostre que este campo de velocidade representa um possível escoamento incompressível.
5.82 Considere o campo de velocidade dado por V → = A x 2 i ^ + B x y j ^ , em que A = 3,3m - 1 s - 1 , B = - 6,6m - 1 s - 1 e as coordenadas são medidas em ft.(a) Determine a rotação do fluido.(b) Av