Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 10.Problemas - Ex. 52
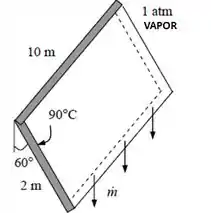
Repita o problema 10-51 considerando a placa inclinada a 60°
Passo 1
Vamos começar tomando as propriedades do vapor na temperatura de saturação, ok? Lembrando que como estamos a 1 atm e se tratando de vapor, essa Tsat e as propriedades da fase gasosa serão tomadas em Tf = (Tsat + Ts)/2 = (100+90)/2 = 95°C
Para a letra (a) o que a gente quer encontrar é o q = hA(Tsat – Ts) e na (b) vamos partir de
Passo 2
(a) Agora a gente precisa calcular o valor de Reynold associado a placa plana, onde L está associado ao eixo que há o escoamento do condensado, ou seja, a altura da placa.
Note, que precisamos encontrar h’fg
Substituindo os valores no Reynold, vamos obter o valor de:
Como estamos num valor entre 30 e 1800, nos encontramos num regime laminar, e com isso vamos usar então a correlação apropriada para placa plana para encontrarmos o coeficiente de transferência de calor, se liga!
Passo 3
Por fim, a gente pega tudo isso que encontramos e calculamos a taxa!!
Passo 4
(b) Agora partiu calcular a taxa de condensação?!!