Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 3.Problemas - Ex. 111

Repita o Problema 3-110 levando em conta a expansão térmica d água â medida que ela é aquecida de 20 ° C até a temperatura de ebulição 100 ° C .

Passo 1

Bem antes de iniciarmos, recomendo fortemente que você de uma olhada na resolução do problema 3 - 110 , e você notará que exercício deseja o peso máximo de água que podemos despejar no bule sem que ele transborde, bem o enunciado nos da informações suficientes para isto, como explanado no problema 3 - 110 . Portanto aqui determinaremos a coluna máxima de água que pode ser despejada.

Vamos lá, assumindo que a quantidade de água no tubo de serviço será desconsiderada e a temperatura da água é de T = 20 ° C .

Passo 2

Utilizando as considerações anteriores, primeiramente temos que determinar a altura total da coluna de água que podemos ter, seria h t o t a l = 4 + x , x este que pode ser determinado por trigonometria.

Temos o seguinte, triangulo retângulo:

cos ⁡ 40 ° = x 12

x = cos ⁡ 40 ° ∙ 12

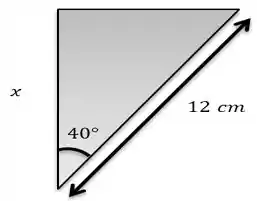
Tendo nosso h t o t a l = 4 + cos ⁡ 40 ° ∙ 12 = 13.2   c m .

Após isto, para determinarmos a coluna de água máxima que podemos colocar seria o seguinte:

h h 2 O , m a x = h t o t a l - Δ H

Passo 3

Temos h t o t a l e agora vamos determinar Δ H , variação está que é dada a partir da pressão manométrica no bule, após isto poderemos calcular o volume máximo de água e com o volume máximo utilizando a formula da densidade da água poderemos determinar a quantidade de peso máximo.

P = ρ w g Δ H

Δ H = P ρ w g = 0,32   k 998 ∙ 9,81 = 0,033   m = 3,3   c m

Agora que temos as colunas que faltavam, para podermos determinar q coluna máxima de e água que pode ser despejada no bule.

h h 2 O , m a x = h t o t a l - Δ H

h h 2 O , m a x = 13,2 - 3,3 = 9,9   c m

Passo 4

Após todo este calculo, temos a variação de volume devido à expansão térmica de 20 ° C para 100 ° C , consultando as tabela (A-4), temos que:

A 20 ° C o volume específico da água:

V 20 ° C = 1 998

A 10 0 ° C o volume específico da água:

V 10 0 ° C = 1 9 57,9

Com isto podes calcular o percentual perdido de volume e com isto determinar a real coluna de água.

V r e d u = V 100 ° C - V 2 0 ° C V 100 ° C = 1 957,9 - 1 9 98 1 957,9 = 0,04 = 4,0 %

Tendo a real coluna de água como:

h h 2 O , m a x = 13,2 - 3,3 = 9,9   c m ∙ 4,0 % = 9,4   c m

Resposta

h h 2 O , m a x = 9,4   c m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Você já deve ter notado que a espessura de uma barragem é maior no fundo. Explique por que as barragens são construídas dessa forma.
Considere uma superfície curva submersa. Explique como você determinaria a componente horizontal da força hidrostática que age sobre essa superfície.
Considere um contêiner cilíndrico vertical parcialmente preenchido com água. Agora o cilindro é posto a girar com relação a seu eixo a uma velocidade angular especificada, e o movimento de corpo rígid
Uma placa retangular com 4 m de altura e 5 m de largura bloqueia a lateral de um canal de água doce com 4 m de profundidade, como mostra a Figura P3-56. A placa tem dobradiças em tomo de um eixo horiz
Considere dois copos idênticos com água, um parado e o outro se movendo em um plano horizontal com aceleração constante. Considerando que não haja derramamento, qual copo terá a pressão mais alta (a)