Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 3.Problemas - Ex. 122

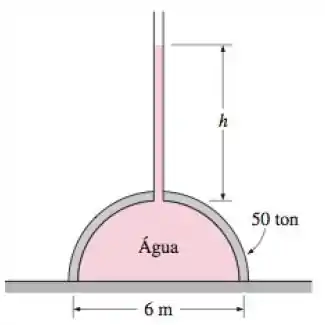
Um domo hemisférico de 50   t o n e diâmetro de 6   m sobre uma superfície nivelada é preenchida com água, como mostra a figura P 3 - 122 . Uma pessoa diz que pode elevar esse domo utilizando a lei de Pascal e acoplando um tubo longo ao topo e preenchendo-o com água. Determine a altura de água necessária no tubo para elevar o domo. Despreze o peso doo tubo e da água que ele contém.

Passo 1

Temos que determinar a coluna de água necessária para elevar o nosso domo.

Para isso vamos assumir que a pressão atmosférica atua nos dois lados do domo, e portanto podemos ignora-la nos nossos cálculos por convenção e também o peso do tubo e da água que está nele serão desprezados.

Tomaremos a densidade da água como padrão de ρ w = 1000   k g / m 3 .

Temos que a água e o domo serão um sistema só.

Quando estamos falando de elevar o domo, a força de reação entre o domo e o chão se torna zero, pois segunda a terceira lei de Newton, para toda força de ação temos uma de reação de mesmo módulo e sentido oposto atuando em corpos diferentes, está não é a definição bonitinha só pra constar. Seguindo o raciocínio, o diagrama de corpo livre do sistema envolve o peso do domo e da água, balanceado pela hidrostática da força de pressão. Seguindo isto podemos igualar estas forças peso e força de hidrostática.

Passo 2

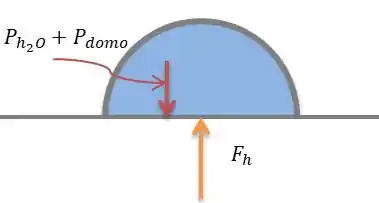
Um humilde desenho do que se passa no nosso domo.

Seguindo a lógica que foi enunciada temos, que o somatório de forças na vertical ou no eixo y , como preferir, fica:

∑ F y = 0

F h = P h 2 O + P d o m o

P ∙ A = m h 2 O ∙ g + m d o m o ∙ g

ρ w g h + R ∙ π R 2 = m h 2 O ∙ g + m d o m o ∙ g

Isolando h , temos:

h = m d o m o + m h 2 O ρ w π R 2 - R

Antes de finalizarmos o calculo temos que determinar a massa da água, como assumimos o domo com um formato de uma meia esfera e temos sua densidade, podemos determinar a massa:

ρ w = m V e s f / 2

m = V e s f / 2 ∙ ρ w

m = 4 π R 3 3 ∙ 2 ∙ 1000

Substituindo na formula de h , temos:

h = 50 ∙ 10 3 + 4 π ∙ 1000 ∙ 3 3 6 1000 ∙ π ∙ 3 2 - 3

h = 0,77   m

Resposta

h = 0,77   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A comporta AB na figura abaixo é uma massa homogênea de 180 kg, 1,2 m de largura, é articulada em A e está apoiada sobre um fundo liso em B. Todos os fluidos estão a 20°C. Para qual profundidade h da
O tanque abaixo tem um tampão de 4 cm de diâmetro no fundo à direita. Todos os fluidos estão a 20°C. O tampão romperá se a força hidrostática sobre ele for de 25 N. Para essa condição, qual será a lei
Encontre a altura H na figura abaixo para qual a força hidrostática sobre o painel retangular é a mesma que a força sobre o painel semicircular abaixo.
Generalizando o problema P2.66 da seguinte maneira: represente a distancia AB por H, a distância BC por L e o ângulo ABC por θ . Considere que o material da barragem tenha densidade d. A largura da ba
Para o cilindro semicircular CDE no Exemplo 2.9, encontre a força hidrostática vertical integrando o componente vertical da pressão sobre a superfície de θ = 0 até θ = π .