Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 3.Problemas - Ex. 126
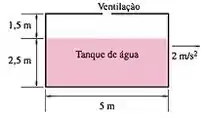
Um tanque com de comprimento e de altura contém água a uma profundidade de quando não está em movimento e é aberto para a atmosfera através de uma ventilação no meio. Agora o tanque é acelerado até a direita em uma superfície nivelada a . Determine a pressão máxima do tanque com relação a pressão atmosférica.
Passo 1
O enunciado quer saber a diferença entre a pressão máxima do tanque e a pressão atmosférica . Para achar esse valor, temos que notar que o nível da água passa a ficar inclinado, quando o tanque é acelerado. A figura abaixo mostra como isso acontece.
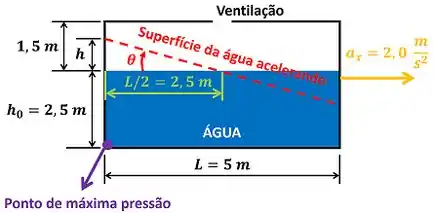
era a altura do nível da água antes de ser acelerada. é a aceleração horizontal da água. A aceleração vertical da água não existe, porque o tanque está apenas sendo acelerado para a direita.
é o ângulo entre a superfície da água parada e a superfície da água acelerada. é a diferença e altura entre o nível máximo da água sendo acelerada e o nível da água sem aceleração.
Podemos ver pela figura que o nível da água do lado esquerdo do tanque possui altura máxima. Isso significa que o lado esquerdo do fundo do tanque possui a maior coluna de água em cima dele (a altura dessa coluna é igual a ). Por isso, o fundo do lado esquerdo tanque está submetido à maior pressão do tanque. Essa pressão vale:
onde é a densidade da água que vale aproximadamente e é a aceleração da gravidade que vale aproximadamente .
Logo, vale:
Só nos resta saber calcular . Aprenderemos isso na próxima etapa.
Passo 2
Podemos ver pela imagem que os lados , e a superfície da água acelerando formam um triângulo. Por isso, podemos calcular a partir do lado e do ângulo através da fórmula abaixo.
A equação do livro mostra como se calcula a tangente do ângulo .
Substituindo a fómula da tangente na fórmula de e a fórmula de na equação de , encontramos:
Com essa equação, podemos iniciar as contas.