Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 7.Problemas - Ex. 12

Repita do Problema 7.11 para o caso no qual a camada-limite é feita turbulenta já na aresta frontal da placa.

Passo 1

Fala galera!!

Para essa questão, podemos desenhar o seguinte esquema para um escoamento turbulento e paralelo em uma placa plana isotérmica de comprimento L .

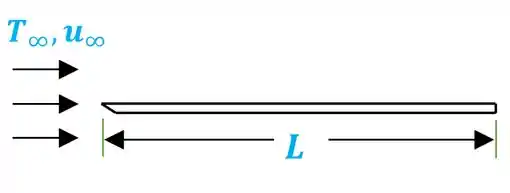
Passo 2

Para começar a resolver essa questão, podemos dizer que em uma placa única pode-se aplicar a equação 7.38, ou seja:

N u - L , 1 = h - L , 1 L k = 0 , 037   R e L , 1 4 / 5 - A P r 1 / 3

Como o escoamento é completamente turbulento desde o inicio, temos que A = 0 . Assim temos que:

N u - L , 1 = h - L , 1 L k = 0,037   R e L , 1 4 / 5 P r 1 / 3

Pela igualdade acima, também podemos dizer que:

h - L , 1 = k L 0,037   R e L , 1 4 / 5 P r 1 / 3

Passo 3

Agora, podemos desenhar o seguinte esquema para um escoamento turbulento e paralelo em uma placa plana isotérmica de comprimento L N , onde L N = L / N . O desenho abaixo ilustra um caso onde N = 3 .

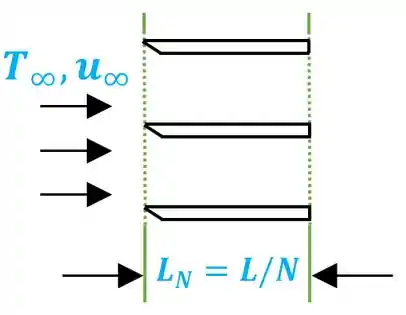
Passo 4

Para e placa plana descrita acima de comprimento L N , também podemos aplicar a equação a 7.38, ou seja:

N u - L , N = h - L , N L N k = 0,037   R e L , N 4 / 5 - A P r 1 / 3

Como o escoamento é completamente turbulento desde o inicio, temos que A = 0 . Assim temos que:

N u - L , N = h - L , N L N k = 0,037   R e L , N 4 / 5 P r 1 / 3

Pela igualdade acima, também podemos dizer que:

h - L , N = k L N 0,037   R e L , N 4 / 5 P r 1 / 3

Também podemos dizer que

R e L , N = R e L , 1 N

Substituindo na equação anterior, temos:

h - L , N = k L N 0,037   R e L , 1 N 4 / 5 P r 1 / 3

Passo 5

Agora, podemos dividir o coeficiente de transferência de calor médio em relação as N placas e o coeficiente de transferência de calor médio sobre toda a placa da seguinte maneira:

h - L , N h - L , 1 = k L N 0,037   R e L , 1 N 4 / 5 P r 1 / 3 k L 0,037   R e L , 1 4 / 5 P r 1 / 3  

Substituindo L N por L / N , temos o seguinte:

h - L , N h - L , 1 = k L / N 0,037   R e L , 1 N 4 / 5 P r 1 / 3 k L 0,037   R e L , 1 4 / 5 P r 1 / 3  

h - L , N h - L , 1 = k N L R e L , 1 N 4 / 5 k L R e L , 1 4 / 5  

h - L , N h - L , 1 = N N 4 / 5  

h - L , N h - L , 1 = N 1 / 5

Portanto, a razão dos coeficientes médios de transferência de calor para fluxo turbulento é

h - L , N h - L , 1 = N 1 / 5

Resposta

h - L , N h - L , 1 = N 1 / 5

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

7 – O comportamento da histerese da curva de ebulição se torna menos pronunciada conforme a diferença entre os fluxos de calor máximo e mínimo se tornam pequenos. Calcule a razão do máximo e mínimo fl
17 – Foi demonstrado experimentalmente que o fluxo de calor critico é altamente dependente da pressão, principalmente através da dependência da pressão da tensão superficial do fluido e do calor laten
Analise detalhadamente as figuras (9.4) e (9.5) .
Considere uma parede plana vertical parada de 1m de altura coberta por uma fina película aderente de água a 30 ° C . Determine o número de Sherwood natural, admitindo que tanto a placa quanto ao ambie
Refaça o exercício anterior considerando a equação ( 9.132 b )