Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 10.Problemas - Ex. 17

17 – Foi demonstrado experimentalmente que o fluxo de calor critico é altamente dependente da pressão, principalmente através da dependência da pressão da tensão superficial do fluido e do calor latente de vaporização. Usando a Eq. 10.6, calcule o valor de q”max para a água em uma superfície grande e horizontal como uma função da pressão. Demonstre que o pico do fluxo de calor crítico ocorre em aproximadamente 1/3 da pressão crítica (pc=221 bar). Desde que todos os fluidos comuns têm essa característica, sugira quais coordenadas deveria ser usada para plotar o fluxo de calor critico versus a pressão para obter uma curva universal.

Passo 1

A Eq. 10.6 é a seguinte

q " m a x = C H v a p ρ v σ g ( ρ l - ρ v ) ρ v 2 0,25

Onde,

-Hvap é entalpia de vaporização do fluido;

-C é uma constante que depende da forma da superfície;

-ρv é densidade do vapor saturado;

-ρl é densidade do liquido saturado;

-g é a constante da gravidade, 9,81 m/s²;

-σ é a tensão superficial do fluido.

Para superfícies grande s e horizontais, C vale

C = 0,149

Passo 2

Para colocarmos o fluxo de calor em função da pressão, vamos ter que expressar as propriedades do fluido saturado (Hvap, ρv, ρl, e σ) em função da pressão. Podemos fazer isso pegando dados da Tabela para a água saturada e extrapolando expressões para cada uma dessas propriedades.

A melhor maneira de se fazer isso é colocar os dados em alguma ferramenta computacional gráfica e pegando a equação que ajusta os dados.

Vamos usar o EXCEL:

Os dados abaixo foram os dados usados para realizar o plote do gráfico, eles foram pegados da tabela A.6 do Incropera:

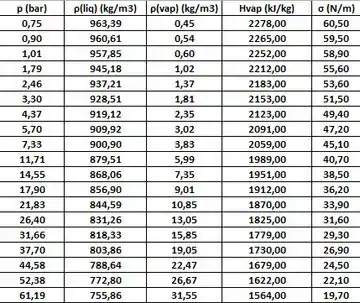
Os seguintes gráficos foram obtidos, com as seguintes equações para o ajuste dos dados para gráfico:

ρ l = - 0,0014 p 3 + 0,1736 p 2 - 8,6504 p + 960,97

ρ v = 0,0005 p 2 + 0,4787 p + 0,1946

H v a p = - 0,0049 p 3 + 0,5896 p 2 - 29,376 p + 2265,1

σ = 2 x 10 - 5 p 4 - 0,0022 p 3 + 0,1128 p 2 - 2,8339 p + 60,941

Passo 3

Agora que você tem todas as propriedades de saturação do fluido em função apenas da pressão, basta agora você pegar a equação do fluxo máximo e substituir essas equações:

q " m a x = C H v a p ρ v σ g ( ρ l - ρ v ) ρ v 2 0,25

Substituindo:

ρ l - ρ v = - 0,0014 p 3 + 0,1736 p 2 - 8,6504 p + 960,97 - 0,0005 p 2 + 0,4787 p + 0,1946

ρ l - ρ v = - 0,0014 p 3 + 0,1731 p 2 - 9,1291 p - 960,78

σ ρ l - ρ v = ( 2 x 10 - 5 p 4 - 0,0022 p 3 + 0,1128 p 2 - 2,8339 p + 60,941 ) ( - 0,0014 p 3 + 0,1731 p 2 - 9,1291 p - 960,78 )

σ ρ l - ρ v = 2,8 x 10 - 8 p 7 + 1,17 x 10 - 5 p 6 - 7,21 x 10 - 4 p 5 + 0,0244 p 4 + 0,5081 p 3 - 71,96 p 2 + 2166,418 p - 58550,9

ρ v 2 = 0,0005 p 2 + 0,4787 p + 0,1946 2

ρ v 2 = 2,5 x 10 - 7 p 4 + 4,79 x 10 - 4 p 3 + 1,95 x 10 - 4 p 2 + 0,1863 p + 0,0379

H v a p ρ v = ( - 0,0049 p 3 + 0,5896 p 2 - 29,376 p + 2265,1 ) ( 0,0005 p 2 + 0,4787 p + 0,1946 )

H v a p ρ v = - 2,45 x 10 - 6 p 5 - 2 x 10 - 3 p 4 + 0,2667 p 3 - 12,815 p 2 + 1078,6 p + 440,79

Passo 4

Substituindo:

q " m a x = 0,149 - 2,45 x 10 - 6 p 5 - 2 x 10 - 3 p 4 + 0,2667 p 3 - 12,815 p 2 + 1078,6 p + 440,79 9,81 2,8 x 10 - 8 p 7 + 1,17 x 10 - 5 p 6 - 7,21 x 10 - 4 p 5 + 0,0244 p 4 + 0,5081 p 3 - 71,96 p 2 + 2166,418 p - 58550,9 2,5 x 10 - 7 p 4 + 4,79 x 10 - 4 p 3 + 1,95 x 10 - 4 p 2 + 0,1863 p + 0,0379 0,25

Chegamos então em uma expressão polinomial para o fluxo máximo em função da pressão

Resposta

q " m a x = 0,149 - 2,45 x 10 - 6 p 5 - 2 x 10 - 3 p 4 + 0,2667 p 3 - 12,815 p 2 + 1078,6 p + 440,79 9,81 2,8 x 10 - 8 p 7 + 1,17 x 10 - 5 p 6 - 7,21 x 10 - 4 p 5 + 0,0244 p 4 + 0,5081 p 3 - 71,96 p 2 + 2166,418 p - 58550,9 2,5 x 10 - 7 p 4 + 4,79 x 10 - 4 p 3 + 1,95 x 10 - 4 p 2 + 0,1863 p + 0,0379 0,25

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere uma célula a combustível delgada com 50 mm × 50 mm similar a do Exemplo 1.5, com ar em escoamento paralelo sobre suas superfícies. Fios com diâmetro muito pequeno são esticados cruzando ambo
Ar forçado a 25 °C e 10 m/s é usado para resfriar componentes eletrônicos montados sobre uma placa de circuito impresso. Considere um chip com 4 mm de comprimento e 4 mm de largura, localizado a 120 m
Ar a pressão atmosférica e a uma temperatura de 25 °C escoa paralelamente, com velocidade de 5 m/s, sobre uma placa plana com 1 m de comprimento que é aquecida com um fluxo térmico uniforme de 1250 W/
Considere ar atmosférico a u ∞ = 2 m/s e T ∞ = 300 K em escoamento paralelo sobre uma placa plana isotérmica de comprimento L = 1 m e temperatura T s = 350 K.(a) Calcule o coeficiente convectivo local
Um chip de silício quadrado (10 mm × 10 mm) é isolado termicamente em um de seus lados e resfriado no lado oposto por ar atmosférico, em escoamento paralelo, com u ∞ = 20 m/s e T ∞ = 24 °C. Quando em