Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 13.Problemas - Ex. 18

Repita o Problema 13.15, considerando que o bocal convergente seja substituído por um bocal convergente-divergente com um diâmetro de saída de 2,5 cm (mesma área de garganta).

Passo 1

Para o cálculo da pressão crítica:

p o p * = k + 1 2 k k - 1

Como:

p 0 = 101   k P a ;

k = 1,4 .

101 p * = 1,4 + 1 2 1,4 1,4 - 1

p * = 53,36   k P a

Passo 2

 Para achar a área do bico convergente:

A = π 4 ⋅ d 2

A = π 4 ⋅ 1 2

A = 0,785   c m 2

Passo 3

Para a área no ponto crítico:

A = π 4 ⋅ d 2

A = π 4 ⋅ 2,5 2

A = 4,91   c m 2

Passo 4

Para encontrar o número de Mach:

A A * = 1 M ⋅ 1 + k - 1 2 ⋅ M 2 k + 1 2 k + 1 2 k - 1

4,91 0,785 = 1 M ⋅ 1 + 1,4 - 1 2 ⋅ M 2 1,4 + 1 2 1,4 + 1 2 1,4 - 1

6,25 = 1 M 1 + 0,2 ⋅ M 2 1,2 3

10,8 ⋅ M = 1 + 0,2 ⋅ M 2 3

M 1 = 0,0931 e M 2 = 3,41

Ou seja, o fluxo é sempre bloqueado.

Passo 5

Colocando os dados do fluxo em tabela, temos:

Desse modo:

Q = 0,0187   k g / s

Resposta

Q = 0,0187   k g / s

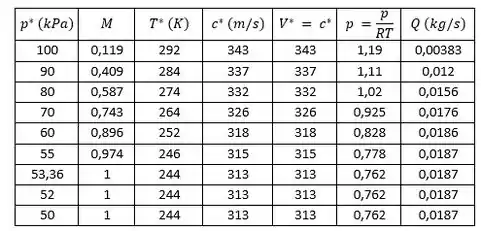
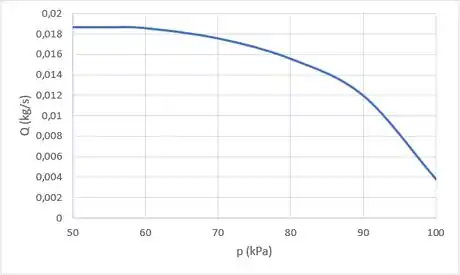
Ver Outros Exercícios desse livro