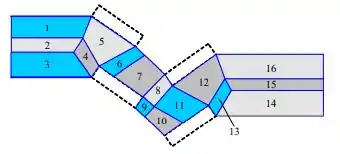
Represente uma malha multiblocos estruturada com blocos elementares de quatro lados para o domínio computacional do Problema 15-24. Cada bloco deve ter células estruturadas de quatro lados, mas você não precisa representar a malha, apenas a topologia do bloco. Tente deixar todos os blocos com a forma mais retangular possível para evitar células com inclinação alta nos cantos. Suponha que o código CFD exija que a distribuição de nós nos pares periódicos dos lados seja idêntico (os dois lados de um par periódico estão “ligados” no processo de geração de malha). Considere também que o código CFD não permita que os lados de um bloco se dividam para a aplicação das condições de contorno.

Fala aí, galera. Tudo bem? Bora pra outra questão.

Escolhemos o domínio computacional da Fig. 1 do problema anterior. Nós esboçamos um possível elementar topologia de bloqueio na Fig. 1 para o caso em que o código CFD requer que a distribuição do nó seja exatamente a mesma em pares periódicos. Também assumimos que não podemos dividir uma borda periódica e não seu parceiro. Os blocos são numerados. Esta topologia tem 16 blocos elementares.

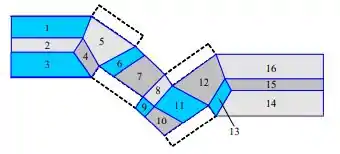
Observe que, com esta topologia de bloqueio, tivemos que dividir o par de limite "médio" periódico em duas arestas (os topos dos blocos 6 e 7 e os fundos dos blocos 9 e 10). Desde que ambos os pares de cada segmento tenham o mesmo tamanho e tenham o mesmo número de nós, isso não é um problema. No código CFD, teríamos de nomear cada par periódico separadamente. Os números dos blocos são identificados. Observe que a maioria dos blocos são quase retangulares, de modo que nenhum dos as células teriam que ser altamente distorcidas.