Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 3.Problemas - Ex. 69

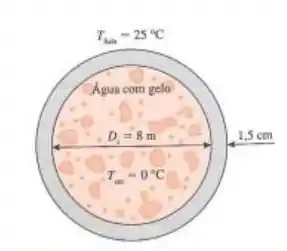
Um reservatório esférico de aço inoxidável k =   15   W   m   ·   K de 8 m de diâmetro interno e 1,5 cm de espessura é usado para armazenar água com gelo a 0°C. O reservatório está localizado em uma sala cuja temperatura é de 25°C. As paredes da sala também estão a 25°C. A superfície externa do tanque é preta (emissividade ε = 1 ), e a transferência de calor entre a superfície externa do tanque e os arredores é por convecção natural e radiação. Os coeficientes de transferência de calor por convecção nas superfícies interna e externa do tanque são de 80   W   m 2   ·   K e 10   W   m 2   ·   K , respectivamente. Determine:

  1. A taxa de transferência de calor para a água gelada no tanque;
  2. A quantidade de gelo a 0°C que derrete durante um período de 24 horas.

O calor de fusão da água à pressão atmosférica é de h i f =   333,7 k J k g .

Passo 1

Beleza galera, vamos lá!!

O que está acontecendo aqui é o seguinte, existe uma troca de calor através da parede do reservatório entre a água gelada armazenada e o ambiente externo.

O ambiente externo também é submetido a radiação emitida pela superfície externa.

Desenhando:

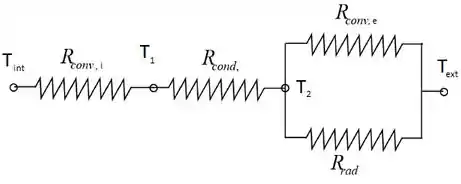
Vamos calcular as resistências?

R c o n v ,   e = 1 h c o n v ,   e × A e x t

R c o n d = R e s f e r a = r 2 - r 1 k × 4 π r 2 r 1

R c o n v , i = 1 h c o n v ,   i × A i n t

R r a d = 1 h r a d × A i n t

Sabemos que R c o n v , e e R r a d estão em paralelo:

1 R 1 = 1 R c o n v , e + 1 R r a d

Substituindo:

1 R 1 = 1 1 h c o n v ,   e x t × A e x t + 1 1 h r a d × A e x t

1 R 1 = A e x t ( h c o n v ,   e x t + h r a d )

Agora a grande questão aqui é qual será a área e o coeficiente de radiação, não é verdade?

Passo 2

Vamos começar pela área externa! Neste caso teremos os 8m de diâmetro interno mais os 3 cm equivalentes à superfície:

A e x t = π d 2 2

A e x t = π 8,03   m 2 = 202,6   m 2

Agora a área interna é fácil:

A i n t = π d 1 2

A i n t = π 8,0   m 2 = 201,06   m 2

Beleza ! Já achamos as áreas, mas agora precisamos do coeficiente de radiação:

h r a d = ε σ ( T 2 2 + T e x t 2 ) ( T 2 + T e x t )

Nós já sabemos que a temperatura externa do reservatório é 25°C:

T e x t = 25 ° C + 273 = 298   K

Não sabemos nada sobre a temperatura da superfície externa, mas vamos assumir que haja troca de calor suficiente e, por isso, a temperatura seja 5°C:

T 1 = 5 ° C + 273 = 278   K

Sabendo que a constante de Boltz é:

σ = 5,67 × 10 - 8 W m 2 K 4

E:

ε = 1

Então:

h r a d = 1 × 5,67 × 10 - 8 W m 2 K 4 ( 298 2 + 278 2 ) ( 298   K + 278 )

h r a d = 5,42 W m 2 K  

Passo 3

Neste passo nós vamos achar a resistência total, só que a convectiva externa e a radiação estão em série nós vamos calcular elas primeiro.

Jogando os dados na fórmula do passo 1:

1 R 1 = 202,6   m 2 10 W m 2 K + 5,42 W m 2 K

R 1 = 0,00032   K W

Como esta resistência está em série com as demais:

R T o t a l = R 1 + R c o n v ,   i + R c o n d

Substituindo:

R T o t a l = 0,00032   K W + 1 8 0   W   m 2   ·   K × 201,06   m 2 + 4,015 m - 4 m 15   W   m   ·   K × 4 π ( 4 m × 4,015 m )

Então:

R T o t a l = 0,0003 87   K W

Agora é só colocar na fórmula do calor:

Q ˙ = ∆ T R T o t a l

Substituindo:

Q ˙ = 25 ° C - 0 ° C 0,000387   K W

Como a variação em graus Celsius é a mesma que a variação em kelvin:

Q ˙ = 64571   W

Já resolvemos a letra a, agora boora pra b!!

Passo 4

Antes de começar a b vamos checar se a temperatura que assumimos ser a da superfície externa é válida, ok?

Para isso usamos a fórmula do calor novamente e a resistência para a superfície externa:

Q ˙ = T e x t - T 1 R 1

Substituindo:

64571   W = 25 ° C - T 1 0,00032   K W

T 1 = 4,34 ° C

Bem próximo do que nós assumimos, então bora continuar!!

Passo 5

Se nós já sabemos quanto de calor é trocado pelo reservatório:

Q ˙ = 64571   W = 64571   J s

Nós precisamos saber quanto calor o reservatório recebe em 24 horas. Transformando em segundos:

∆ t = 24   h × 3600   s 1   h = 86400   s

Sendo assim:

Q = Q ˙ ∆ t

Q = 64571   J s × 86400   s = 5,58 × 10 9   J

Para derreter o gelo nós usamos calor de fusão:

Q = m h i f

Isolando a massa:

m = Q h i f

m = 5,58 × 10 9   J 333,7 × 10 3 J k g = 16718 ,   4   k g

E é isso aí galera !

Bora pra próxima?

Resposta

  1. 64571   W ;
  2. 16718 ,   4   k g .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O que é o raio crítico do isolamento? Como é definido para uma camada cilíndrica?
Considere um tubo a uma temperatura constante cujo raio seja maior que o raio crítico de isolamento. Alguém alega que a taxa de perda de calor do tubo aumentou quando algum isolamento é adicionado ao
Considere um tubo isolado exposto à atmosfera. O raio crítico do isolamento será maior em dias calmos ou em dias ventosos? Por quê?
Repita o Problema 3–84 para oxigênio líquido, que tem uma temperatura de ebulição de -183°C, calor de vaporização de 213 k J k g e densidade de 1140 k g m 3 a 1 atm de pressão.
Repita o Problema 3-80, considerando que a camada de 0,25 cm de espessura de depósito mineral k = 0,87Wm· K se formou sobre a superfície interna do tubo.