Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 3.Problemas - Ex. 63

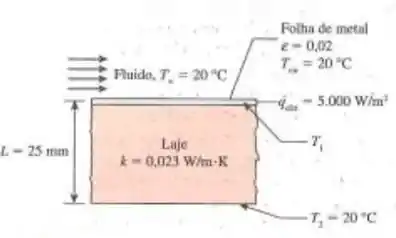
Um experimento para medir coeficientes de transferência de calor por convecção foi montado com uma única folha de metal muito fina de emissividade muito baixa (por exemplo, cobre polido) fixada na superfície de uma laje de material com baixa condutividade térmica. A outra superfície da folha de metal é exposta à transferência de calor por convecção, pelo fluxo de fluido sobre a superfície da folha. Essa configuração diminui a condução de calor através da laje e a radiação sobre a superfície da folha de metal, enquanto a convecção de calor desempenha o papel de destaque. A laje na qual a folha de metal está fixada tem uma espessura de 25 mm e uma condutividade térmica de 0,023   W m . K . Em uma condição em que a temperatura ambiente ao redor é de 20°C, a folha de metal é aquecida eletricamente com um fluxo de calor uniforme de 5000 W m 2 . Se a superfície inferior da laje for de 20°C e a folha de metal tiver uma emissividade de 0,02, determine:

  1. O coeficiente de transferência de calor por convecção se o ar estiver fluindo sobre a folha de metal e a temperatura da superfície for de 150°C;
  2. O coeficiente de transferência de calor por convecção se a água estiver fluindo sobre a folha de metal e a temperatura da superfície da folha for 30°C.

Passo 1

Apesar do tamanho desta questão não se assustem !!

Vamos pensar no que está acontecendo aqui!!

Temos a laje conduzindo três formas diferentes de calor: radiação e a eletricidade proveniente da placa, e a convectiva que transfere calor à placa, ok?

Então nós teremos estas três formas de calor se igualando a condução, certo?

Q r a d i a ç ã o ˙ + Q c o n v e c ç ã o ˙ + Q e l é t r i c a ˙ = Q c o n d u ç ã o ˙

Vamos tentar representar mais ou menos como vai funcionar este esquema:

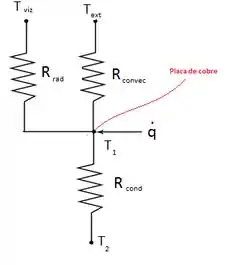
Então, vamos colocar estas informações na fórmula que descobrimos:

T e x t - T 1 R c o n v + T v i z - T 1 R r a d + q ˙ A = T 1 - T 2 R c o n d

Vamos isolar a resistência de convecção, porque precisamos do coeficiente né?

1 R c o n v = T 1 - T 2 R c o n d - T v i z - T 1 R r a d - q ˙ A × 1 T e x t - T 1  

Sabemos que:

R r a d = 1 h r a d A

R c o n v = 1 h c o n v A

R c o n d = L h c o n d A

Substituímos:

1 1 h c o n v A = T 1 - T 2 L h c o n d A - T v i z - T 1 1 h r a d A - q ˙ A × 1 T e x t - T 1

Olha que legal, já podemos remover a área, já que ela está no denominador de todos os termos:

h c o n v = T 1 - T 2 L h c o n d - T v i z - T 1 1 h r a d - q ˙ × 1 T e x t - T 1

Vamos guardar esta informação e procurar as demais que ainda não temos!!

Passo 2

O que nós ainda não temos?

Só o coeficiente de radiação!!

E ele é dado por:

h r a d = ε σ ( T s u p e r f í c i e 2 + T v i z 2 ) ( T s u p e r f í c i e + T v i z )

A constante de Boltz ( σ ) será 5,67 × 10 - 8 W m 2 . K 4 e a emissividade ( ε ), 0,02.

Agora só falta transformar as temperaturas para kelvin, já que aqui temos uma variação ao quadrado:

T v i z = 20 ° C + 273 = 293   K

Para a letra a:

T s u p e r f í c i e = T 1 = 150 ° C + 273 K = 423   K

Então:

h r a d = 0,02 5,67 × 10 - 8 W m 2 . K 4 ( 423 2 + 293 2 ) ( 423 + 293 )

h r a d = 0,215   W m 2 . K

Substituindo tudo na fórmula do passo 1:

h c o n v = 150 - 20 K 0,025   m 0,023 W m . K - 20 - 150 K 1 0,215   W m 2 . K - 5000 W m 2 × 1 ( 20 - 150 ) K

Atenção aqui galera! Não transformei em kelvin aqui porque temos uma variação simples, tudo bom?

h c o n v = 37,3 W m 2 . K  

Beleza!! Já temos a resposta para a letra a !

Passo 3

Na letra b teremos uma temperatura da superfície diferente:

T s u p e r f í c i e = T 1 = 30 ° C + 273 K = 303   K

Então:

h r a d = 0,02 5,67 × 10 - 8 W m 2 . K 4 ( 303 2 + 293 2 ) ( 303 + 293 )

h r a d = 0,1201   W m 2 . K

Substituindo tudo na fórmula do passo 1:

h c o n v = 30 - 20 K 0,025   m 0,023 W m . K - 20 - 30 K 1 0,1201   W m 2 . K - 5000 W m 2 × 1 ( 20 - 30 ) K

h c o n v = 499 W m 2 . K  

E é isso aí galeraaa!!

Resposta

  1. 37,3 W m 2 . K ;
  2. 499 W m 2 . K .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

13 - Uma casa possui uma parede composta com camadas de madeira, isolamento à base de fibra de vidro e placa de gesso, como indicado no esboço. Em um dia frio de inverno, os coeficientes de transferên
14 - Seja a parede composta do Problema 3.13 sob condições nas quais o ar interior ainda é caracterizado por T ∞ , i = 20 ℃ ℃ e h i = 30W / ( m 2 · K ) . Entretanto, use condições mais realistas para
1 - Considere a parede plana da Figura 3.1, que separa dois fluidos, um quente e o outro frio, a temperaturas T ∞ , 1 e T ∞ , 2 , respectivamente. Usando balanços de energia nas superfícies x = 0 e x
As janelas de vidro de um automóvel têm área superficial A = 2,6 m2 e espessura t = 4 mm. A temperatura externa é de T∞,e = 32°C, enquanto o compartimento dos passageiros é mantido a T∞,i = 22°C. O co
A superfície superior de um compartimento aquecido possui uma porção muito lisa (A) e outra acentuadamente rugosa (B), e encontra-se em contato com uma corrente de ar atmosférico. Com o interesse de m