Exercícios de Condução em Sistemas Radiais - Lista de Exercícios Resolvida

(Adaptada) Um tanque esférico para armazenar oxigênio líquido no ônibus espacial deve ser construído em aço inoxidável () com de diâmetro e de espessura de parede. O ponto de ebulição e o calor latente de fusão do oxigênio líquido são e respectivamente. O tanque será instalado em um grande compartimento cuja temperatura deve ser mantida a . Projete um sistema de isolamento térmico capaz de manter as perdas de oxigênio por evaporação abaixo de . Admita que a condutividade do isolamento equivale a e considere a resistência de convecção desprezível frente às demais resistências térmicas.

Um reservatório esférico armazena um gás a temperatura de . A parede do reservatório é composta de aço e tem uma espessura igual a .

Deseja-se adicionar um material isolante, de forma a reduzir a perda de calor do reservatório em . Determine a espessura necessária de isolante, considerando que a sua condutividade térmica vale . Considere o coeficiente de troca de calor interno igual a , e o externo igual a , e temperatura ambiente de .

Existe a possibilidade de que no caso de uma tubulação, aumente-se a espessura de um certo isolante e isso aumente a transferência de calor ao invés de diminuir, tal como seria desejado ao aumentar a espessura de qualquer isolante. Isso nunca acontece quando a geometria é uma placa plana.

Explique o porquê, justificando MATEMATICAMENTE a sua resposta.

Uma casca esférica composta, com raio interno é construída de chumbo () de raio externo e aço inoxidável () de raio externo . A cavidade é preenchida com resíduos radioativos que geram calor a uma taxa de . Propõe-se que o recipiente seja submerso em águas oceânicas que estão a uma temperatura e fornecem um coeficiente de convecção uniforme para a superfície externa do contêiner. Existe algum problema associado a essa proposta?

Admita que a temperatura de fusão dos materiais são: e .

Uma corrente elétrica de flui através de um cabo de aço inoxidável de diâmetro e resistência elétrica de (ou seja, por metro de comprimento de cabo). O cabo encontra-se em um ambiente que está a uma temperatura de , e o coeficiente total de transferência de calor, associado à convecção entre o cabo e o ambiente, é de aproximadamente .

Se o cabo estiver desencapado, qual será a temperatura em sua superfície?

Se um revestimento delgado for aplicado sobre o cabo, com uma resistência térmica de contato de , quais serão as temperaturas das superfícies do isolamento e do cabo?

Há preocupação em relação à capacidade do isolamento em suportar temperaturas elevadas. Qual a espessura do isolamento () que produzirá o menor valor para a temperatura máxima na camada de isolamento? Qual será o valor da temperatura máxima quando essa espessura de isolamento for utilizada?

Uma semiesfera (uma esfera cortada pela metade) que estava com uma temperatura inicial teve sua face plana colocada sobre uma placa mantida a temperatura e esse conjunto foi colocado em um meio fluido a uma temperatura que é menor que .

Esse meio fluido está a uma velocidade bem caracterizada de tal forma que existe um coeficiente de película médio, , muito bem definido.

Partindo da equação geral de transferência de calor, equacione o modelo o modelo do perfil de temperatura da semiesfera e modele também a condições de contorno e iniciais. Utilize o sistema de coordenadas mais conveniente para a resolução do problema.

Justifique cada simplificação. Seja sucinto. NÃO RESOLVA A EQUAÇÃO, APENAS MODELE.

Um vaso esférico de aço inoxidável , com de diâmetro interno e de espessura de parede, é usado como reator químico.

A superfície externa do reator é resfriada por ar com temperatura de e coeficiente de transferência de calor de . No regime permanente, deseja-se saber.

Qual a taxa de calor transferida para o ar, sabendo-se que a temperatura da superfície interna do vaso e de ?

Qual a taxa volumétrica média de geração de energia no interior do reator?

Utilizando a taxa de geração de energia calculada no item e supondo que uma camada de de espessura de fibra-de-vidro seja usada para isolar o reator, responda qual é a temperatura da superfície interna do reator. O contato entre o isolante e parede do reator é suposto perfeito.

Considere um fio elétrico longo com raio e condutividade térmica de . Por conta da corrente elétrica no fio, calor é gerado a uma taxa volum��trica uniforme .

O fio é revestido por um isolante elétrico cerâmico de de espessura, cuja condutividade térmica é de . A temperatura da superfície externa do isolante é .

Supondo propriedades termofísicas constantes e contato perfeito entre o fio e o isolante, no regime permanente, calcule:

Fluxo de calor na superfície externa do isolante elétrico;

Temperatura na interface entre o fio e o isolante;

Temperatura no centro do fio.

Forneça a formulação matemática para o problema de condução de calor em um cilindro oco de raio interno , raio externo e altura , que encontra-se inicialmente na temperatura uniforme .

Uma das superfícies de topo do cilindro é aquecida por um fluxo de calor uniforme , enquanto a outra superfície de topo é isolada termicamente.

O cilindro troca calor internamente por convecção com um meio na temperatura , com coeficiente de transferência de calor . O cilindro troca calor através de sua superfície lateral externa com um meio na temperatura , com coeficiente de transferência de calor .

As temperaturas dos meios externo e interno, assim com os coeficientes de transferência de calor por convecção, são uniformes. Não há geração interna de energia no cilindro.

Uma parede cilíndrica é composta de dois materiais de condutividades térmicas e que são separados por um aquecedor elétrico delgado, para o qual as resistências de contato na interface são desprezíveis.

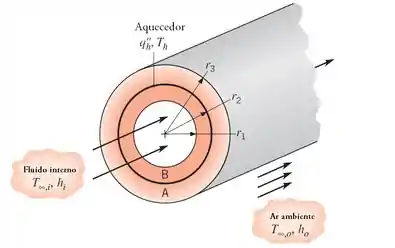
O líquido bombeado através do tubo encontra-se a uma temperatura e fornece um coeficiente de convecção na superfície interna da composição. A superfície externa é exposta ao ar ambiente, que está a e fornece um coeficiente de convecção . Em condições de regime estacionário, um fluxo de calor uniforme é dissipado pelo aquecedor.

Esboce o circuito térmico equivalente do sistema e expresse todas as resistências em termos das variáveis relevantes.

Obtenha uma expressão que pode ser utilizada para determinar a temperatura do aquecedor ().

Obtenha uma expressão para a razão entre os fluxos de calor para os fluidos interno () e externo (). Como as variáveis do problema podem ser ajustadas para minimizar essa razão?

(Adaptado) Um tanque esférico de m de diâmetro contém gás de petróleo liquefeito a . Um isolante de condutividade térmica igual a e espessura de é utilizado para reduzir o ganho de calor pelo gás.

Determine a posição radial na camada do isolante na qual a temperatura atinge , considerando que a temperatura ambiente vale e o coeficiente convectivo de troca de calor externo vale .

(Adaptada) Um tubo de aço de paredes finas com de diâmetro é utilizado para transportar vapor saturado a uma pressão de através de um ambiente onde a temperatura do ar é e o coeficiente de convecção na superfície externa do tubo é . A resistência convectiva do lado vapor pode ser desprezível.

Qual é a perda de calor por unidade de comprimento para o tubo sem isolamento? A emissividade do aço pode ser considerada .

Encontre a equação que descreve a temperatura da superfície externa do isolamento em função dos parâmetros conhecidos (polinômio de quarto grau) se uma camada de isolamento térmico ( e ) com de espessura for aplicada ao redor do tubo.

Após resolver o polinômio de quarto grau, você achou uma temperatura de . Estime a perda de calor com o isolamento.