Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 1.Problemas - Ex. 27

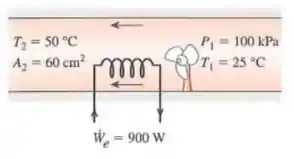
Um secador de cabelo é basicamente um duto no qual são colocadas algumas camadas de resistências elétricas. Um pequeno ventilador puxa o ar e o força a fluir sobre os resistores onde é aquecido. O ar entra em um secador de cabelo de 900 W a 100 kPa e 25°C e sai a 50°C. A área da seção transversal do secador de cabelos na saída é de 60 cm². Negligenciando a energia consumida pelo ventilador e as perdas de calor através das paredes do secador de cabelo, determine (a) a vazão volumétrica de ar na entrada e (b) a velocidade do ar na saída.

Passo 1

Bora pra mais uma??

Então vamo que vamoooo ...

Queremos a vazão volumétrica do ar na entrada, certo?

Para descobrir vamos usar a equação do gás ideal um pouquinho modificada:

P e v e n t r a ˙ = m e n t r a ˙ R T e

Isolando a vazão volumétrica:

v e n t r a ˙ = m e n t r a ˙ R T e P e

Vamos ver o que temos?

T e = 25 ° C + 273 = 298   K

P e = 100   k P a

E tabelado nós temos:

R = 0,287 k J k g K

Só não temos a vazão mássica, então bora achar, ok?

Passo 2

Para calcular a vazão mássica nós precisamos do balanço energético, se estamos negligenciando a energia consumida pelo ventilador e as perdas de calor através das paredes do secador de cabelo

W e n t r a ˙ = Q s a i ˙

A taxa de transferência do calor é fácil:

Q s a i ˙ = m ˙ C p T 2 - T 1

Sendo assim:

W e n t r a ˙ = m ˙ C p T 2 - T 1

Vamos ver o que temos?

W e n t r a ˙ = 9 00   W = 0 , 9   k W

T 1 = 25 ° C

T 2 = 5 0 ° C

Tabelado nós temos:

C p = 1,005 k J k g K

Agora ficou fácil, é só substituir:

0,9   k W = m ˙ 1,005 k J k g K 5 0 ° C - 25 ° C

m ˙ = 0,0357 k g s

Lançando na fórmula do Passo 1:

v e n t r a ˙ = 0,0357 k g s 0,287 k J k g K 298   K 100   k P a

v e n t r a ˙ = 0,03053   m 3 s

Então a vazão volumétrica que entra no duto é de 0,03053   m 3 s .

Simbora pra letra (b)??

Passo 3

Na letra (b) nós queremos a velocidade do ar na saída, certo?

Mas como?

Usando a equação da continuidade:

ρ e n t r a A e n t r a V e n t r a = ρ s a i A s a i V s a i

Aqui é importante vocês lembrarem que:

A 1 V 1 = v e n t r a ˙

Então:

ρ e n t r a v e n t r a ˙ = ρ s a i A s a i V s a i

Olhando as propriedades do ar tabeladas para as temperaturas de entrada e saída:

ρ e n t r a = 1,184 k g m 3

ρ s a i = 1 , 092 k g m 3

Nós temos que:

A s a i = 60   c m ² × 1   m ² 1 0000   c m ² = 0,006   m ²

Então:

1,184 k g m 3 0,03053   m 3 s = 1,092 k g m 3 0,006   m ² V s a i

V s a i = 5,51 m s

Gostaram?!

Resposta

  1. v e n t r a ˙ = 0,03053   m 3 s ;
  2. V s a i = 5,51 m s .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Qual é o método padrão para testar a resolução de malha adequada usando a CFD?
Escreva uma breve discussão (algumas linhas) sobre o signiflcado de cada um dos itens a seguir com relação a uma solução CFD iterativa: ( a ) condições iniciais ( b ) resíduo, ( c ) iteração, ( d ) pó
Suponhamos que você use a CFD para simular o escoamento através de um duto no qual há um cilindro circular como na Figura P15-6C. O duto é longo, mas para economizar recursos computacionais você escol
Das condições de contorno discutidas neste capítulo, liste todas aquelas que podem ser aplicadas ao lado direito do domínio computacional bidimensional representados na Figura P15-9C. Por que as outra
Considere o Problema 15-12C novamente, exceto que a condição de contorno no lado comum entre os blocos 1 e 2 será um ventilador com uma elevação de pressão especificada da direita para a esquerda do v