Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 12.Exercício - Ex. 40

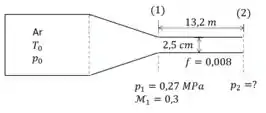
Seja um conduto isolado termicamente de 13,2 m de comprimento e 2,5   c m de diâmetro. O coeficiente de perda de carga distribuída médio é f = 0,008 . Sabendo que na seção de entrada (1) o número de Mach é 0,3 e a pressão é 0,27   M P a   ( a b s ) e que o fluido que escoa é ar, determinar a queda de pressão entre a entrada e a saída.

Passo 1

Vamos utilizar o número de Mach na Tabela 3 e determinar o valor de escoamento e da relação de pressão

M 1 = 0,3   ⇒ T a b e l a   3 f L m á x D H 1 = 5,299 p 1 p * = 3,619

Podemos usar a relação de pressão para determinar a pressão crítica:

p 1 p * = 3,619

p * = p 1 3,619

p * = 0,27 3,619

p * = 0,0764   M P a

Passo 2

E agora podemos usar a equação 12.95 para determinar o valor de f L m á x D H 2

f L m á x D H = f L m á x D H 1 - f L m á x D H 2

f L m á x D H 2 = f L m á x D H 1 - f L m á x D H

f L m á x D H 2 = 5,299 - 0,008 ⋅ 13,2 0,025

f L m á x D H 2 = 5,299 - 4,224

f L m á x D H 2 = 1,075

Passo 3

Agora voltamos à tabela 3 Para determinar o número de Mach e a relação de pressão

f L m á x D H 2 = 1,075 ⇒ T a b e l a   3 M 2 = 0,50 p 2 p * = 2,138

A pressão em (2) é

p 2 p * = 2,138

p 2 = 2,138 ⋅ p *

p 2 = 2,138 ⋅ 0,0764

p 2 = 0,1633   M P a

Passo 4

Finalizamos calculando a diferença entre as pressões:

Δ p = p 1 - p 2

Δ p = 0,27 - 0,163

Δ p = 0,107   M P a

Resposta

Δ p = 0,107   M P a

Ver Outros Exercícios desse livro