Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 6.Problemas - Ex. 34
Seja o nanofluido do Exemplo 2.2.
(a) Calcule os números de Prandtl do fluido base e do nanofluido, usando informações fornecidas no problema exemplo.
(b) Para uma geometria com uma dimensão característica fixa L, e com uma velocidade característica também fixa V, determine a razão entre os números de Reynolds associados aos dois fluidos, Renf/Refb. Calcule a razão entre os números de Nusselt médios, L,nf / L,fb, que está associada a coeficientes de transferência de calor médios idênticos para os dois fluidos, nf = fb.
(c) A dependência funcional do número de Nusselt médio em relação aos números de Reynolds e de Prandtl para um amplo conjunto de várias geometrias pode ser representada de uma forma geral por
sendo C e m constantes, cujos valores dependem da geometria a partir ou para a qual a transferência de calor por convecção ocorre. Na maioria das condições o valor de m é positivo. Para m positivo, é possível que o fluido base forneça taxas de transferência de calor convectivas maiores do que o nanofluido, para condições envolvendo uma geometria fixa, as mesmas velocidades características e temperaturas ambiente e superficial idênticas?
Passo 1
Vamos lá gente!! (a) Os números Prandtl para a água e o nanofluido são:
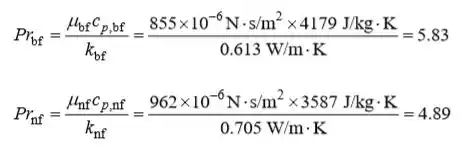
Passo 2
(b) Para uma determinada velocidade e comprimento característico,
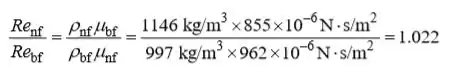
Para os mesmos coeficientes de transferência de calor por convecção,
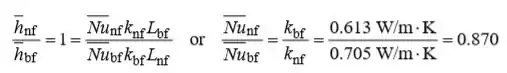
Passo 3
(c) Para que o fluido base tenha uma maior taxa de transferência de calor por convecção, seria necessário . Usando a relação fornecida na declaração do problema,
Portanto, concluímos que o fluido base não proporcionaria maiores taxas de transferência de calor por convecção do que o nanofluido, desde que m seja positivo.