Seja o produto farmacêutico do Problema . Antes de finalizar o processo de fabricação, testes são realizados para determinar experimentalmente a dependência da vida de prateleira do remédio em relação à temperatura de esterilização. Assim, a temperatura de esterilização deve ser cuidadosamente controlada nos testes. Para promover uma boa mistura do fármaco e, desta maneira, uma temperatura de saída relativamente uniforme na seção transversal de saída do tubo, os experimentos são realizados usando um dispositivo constituído por duas serpentinas entrelaçadas, cada uma com diâmetro de tubo de . Os tubos de parede delgada estão soldados em um bastão sólido com alta condutividade térmica e diâmetro de . Uma serpentina transporta o produto farmacêutico com uma velocidade média de e uma temperatura de entrada de , enquanto na segunda serpentina passa água líquida pressurizada com e uma temperatura de entrada de . As serpentinas não entram em contato entre si, mas estão soldadas no bastão de metal, com cada serpentina dando voltas ao redor do bastão. A parte externa do dispositivo é termicamente isolada.

(a) Determine a temperatura de saída do produto farmacêutico. Estime as propriedades da água líquida a .
(b) Investigue a sensibilidade da temperatura de saída do fármaco em relação à velocidade da água pressurizada na faixa .
Passo 1
Vamos lá! Nosso problema nos pede as taxas de aquecimento e refrigeração para dois tipos de canais e comparar os processos, mas antes vamos fazer um esboço do nosso problema para facilitar nossa vida.
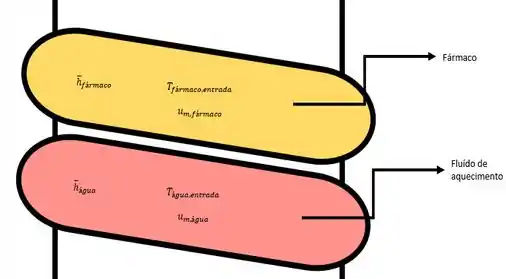
Canal do tipo reto
Agora precisamos fazer nossas famosas considerações. Hehe (u.u)
Passo 2
(a)
Vamos lá, vamos usar os dados da tabela , para a água à e os dados do fármaco são dadas na questão
Para a água:
Para o fármaco:
O escoamento do fármaco é laminar, tendo em vista que , (qualquer dúvida quanto a isso dá uma olhadinha no problema ).
Para o escoamento da água:
Como , o escoamento do fluído de aquecimento é laminar como para ambos os fluídos temos que.
Como da equação temos:
Assim a equação fica:
Como , temos que.
Usando a formula para encontrarmos as temperaturas de saída, temos:
Assim encontramos nossas temperaturas:
Assim temos um sisteminha de duas equações e duas variáveis, a temperatura de superfície e a temperatura de saída, para ambos os fluídos, substituindo temos:
Do balanço de energia para as duas situações temos:
Como estamos considerando a perca de calor pra vizinhança desprezível a resistência térmica das paredes do tubo desprezíveis também, todo calor que sai de um fluído vai para o outro, então , resolvendo qualquer uma das equações do balanço chegamos a:
Passo 3
(b)
Agora vamos analisar como a velocidade da água afeta a temperatura do fármaco, analisando as equações da vazão mássica e do calculo do número de Reynolds temos:
Assim vemos a velocidade é diretamente proporcional ao número de Reynolds, que por sua vez:
Podemos observar que é diretamente proporcional a relação de Whitaker, que é diretamente proporcional ao coeficiente convectivo, logo temos a seguinte relação.
Que por sua vez:
Como a exponencial é negativa, o com aumentando a exponencial tende a zero e:
Então o aumento da velocidade aumenta nossa temperatura de saída que eventualmente vai se estabilizar até virar constante, jogando esses dados em um software de sua preferência, temos:
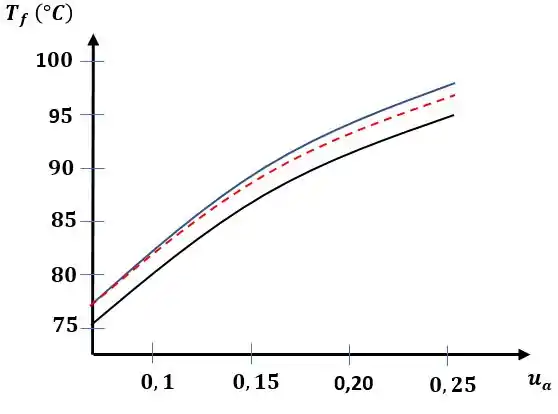
A linha azul representa a temperatura de saída da água, a linha vermelha pontilhada determina a temperatura de superfície das serpentinas e a linha preta representa a temperatura do fármaco.
Isso é tudo pessoal! \o/

Resposta
(a)
(b) Gráfico vide passo-a-passo.