Um resfriador baioneta é usado para reduzir a temperatura de um fluido farmacêutico. O fluido farmacêutico escoa através do resfriador, que é fabricado com um tubo de parede delgada, com diâmetro de , e tem duas seções retas com comprimento de e uma serpentina, com seis voltas e meia, cujo diâmetro da serpentina é de . Um refrigerante escoa no lado externo do resfriador, com um coeficiente convectivo na superfície externa de e uma temperatura de . Considere a situação na qual o fluido farmacêutico entra a , com uma vazão mássica de . O fluido farmacêutico tem as seguintes propriedades: , , e .

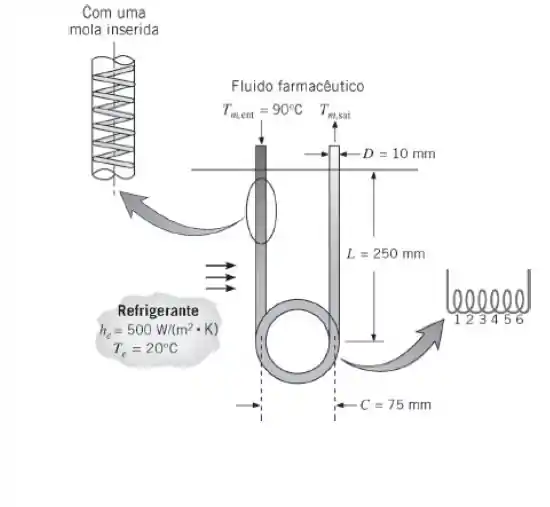
(a) Determine a temperatura de saída do fluido farmacêutico.

(b) Deseja-se reduzir mais a temperatura de saída do fármaco. Entretanto, como o processo de resfriamento é somente uma parte de uma operação de processamento complicada, as vazões não podem ser modificadas. Um engenheiro jovem sugere que a temperatura de saída pode ser reduzida através da inserção de molas helicoidais de aço inoxidável nas seções transversais do resfriador, com base no fato de que as molas irão romper o escoamento adjacente à parede interna do tubo e, deste modo, aumentar o coeficiente de transferência de calor nessa parede interna. Um engenheiro sênior afirma que a inserção das molas poderia dobrar o coeficiente de transferência de calor nas paredes internas retas do tubo. Determine a temperatura de saída do fluido farmacêutico com as molas no interior dos tubos, supondo que o engenheiro sênior esteja correto na sua afirmação.

(c) Você esperaria que a temperatura de saída do fármaco dependesse da forma de orientação das espirais das molas? Por quê?

(a)

Vamos lá! essa letra é meio chata pois temos que analisar o tubo parte por parte, assim temos:

Primeiro precisamos calcular o número de Reynolds, usando os dados do fluido farmacêutico que são dados, temos:

Como o numero de Reynolds é baixo nosso escoamento é laminar! Agora vamos calcular a que distancia da entrada nosso escoamento estará totalmente desenvolvido:

Como , podemos usar as equações e , assim temos:

Como , temos que , agora podemos usar a equação para calcularmos a temperatura na saída da primeira seção, logo antes de entrar na espiral!

Onde:

Assim temos:

(a) continuação

O número critico de Reynolds para a seção espiral é dado pela equação , assim temos:

Como , como , o escoamento ainda deverá ser laminar, 0comprimento da seção é dada por , e como temos que o comprimento necessário para chegarmos ao escoamento com desenvolvimento completo em seções espirais tende a ser entre à menor podemos usar a equação com os coeficientes:

Assim:

Como , temos que , agora podemos usar a equação para calcularmos a temperatura na saída da segunda seção, logo antes de entrar na segunda seção reta!

Como a temperatura de entrada é a temperatura de saída da seção 1, temos:

Onde:

Assim temos:

(a) continuação

Como o coeficiente convectivo da terceira seção é o mesmo da primeira seção e só precisamos utilizar a equação sabendo que a temperatura de entrada é a mesma temperatura de saída da segunda seção, assim temos:

Terminamos o primeiro item. \o/

(b)

Essa parte é mais tranquila, só precisamos refazer as temperaturas com o valor de , dobrado nas seções retas, assim:

Agora seguindo a mesma lógica da letra (a), temos;

Lembrando que é igual pra primeira e terceira seção, e .

(c) Sim, pois o resfriador de baioneta introduz um pequeno efeito de redemoinho que acabaria afetando na seção espiral do tubo, mas essa alteração seria pequena!

Isso é tudo pessoal! \o/