Um arranjo de tubos concêntricos, para o qual os diâmetros interno e externo são e , respectivamente, é usado para remover calor de uma reação bioquímica ocorrendo em um tanque de repouso com de comprimento. Calor é gerado uniformemente no interior do tanque a uma taxa de e uma vazão de de água passa pela região anular.

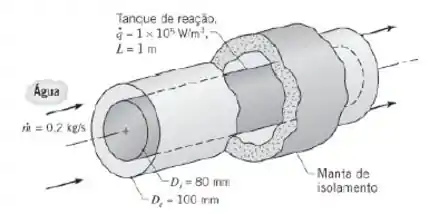
(a) Determine a temperatura de entrada da água vinda do suprimento que irá manter uma temperatura da superfície do tanque média de . Suponha o escoamento e as condições térmicas plenamente desenvolvidas. Esta hipótese é razoável?

(b) Deseja-se ter um leve gradiente axial de temperatura na superfície do tanque, pois a taxa da reação bioquímica é altamente dependente da temperatura. Esboce a variação axial das temperaturas da água e da superfície no sentido do escoamento para os dois casos a seguir: as condições plenamente desenvolvidas da parte , e condições nas quais os efeitos de entrada são importantes. Comente sobre as características das distribuições de temperaturas. Qual mudança no sistema ou nas condições operacionais você faria para reduzir o gradiente da temperatura superficial?

(a)

Vamos lá, vamos usar os dados da tabela para a água, fazendo o balanço de energia temos que o balanço de energia por dois tubos concêntricos é:

Do balanço de energia do tanque de reação temos:

é o diâmetro do tanque de reação, a equação de convecção aplicada a superfície interior é dada por:

Onde é a temperatura média da superfície interior, dada por:

Agora precisamos deixar explícito o comportamento do fluxo para podermos caracterizar nosso coeficiente convectivo, analisando o comportamento do escoamento temos:

Onde , substituindo tudo temos:

Substituindo pelos valores numéricos temos:

Como o número de Reynolds está abaixo do valor critico nosso escoamento é laminar, assim da tabela e da equação com .

Assim usando os dados da tabela , da equação :

Fazendo o mesmo para as equações e temos.

Assim finalmente temos para que o anel interno, o efeito de comprimento da entrada térmica é dado por:

Como o comprimento do cano , como que os efeitos de entrada são significantes! Assim a consideração de escoamento totalmente desenvolvido é aproximada.

(b)

Vamos lá, como a água está passando pela tubulação e sofrendo aquecimento constante então o aumento da temperatura será linear levando em conta a condição de escoamento perfeitamente desenvolvido.

Já se considerarmos o efeito de comprimento da entrada, o coeficiente convectivo da entrada vai ser maior o que aumenta o efeito da convecção fazendo com que a diferença da temperatura entre o fluido e a superfície reduza com maior facilidade, assim os gráficos de temperatura vão ficar assim:

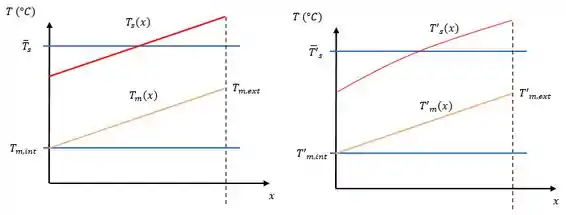
Isso é tudo pessoal! \o/