Uma superfície quente a 1 deve ser resfriada fixando-se aletas de pino de alumínio de de comprimento, de diâmetro e com distância de centro a centro de . A temperatura do meio circundante é , e o coeficiente combinado de transferência de calor nas superfícies é . Pressupondo uma transferência de calor permanente unidimensional ao longo da aleta e um espaçamento nodal de , determine a formulação de diferenças finitas desse problema, as temperaturas nodais ao longo da aleta, resolvendo as equações, a taxa de transferência de calor a partir de apenas uma aleta e a taxa de transferência de calor a partir da seção da placa de .
Passo 1
Muito bem! vamos primeiro pegar os dados do exercício, eu os separei aqui:
Agora feito isso, precisamos encontrar a quantidade de nós a partir do nosso espaçamento nodal.
A temperatura na base é o nosso próprio . A representação do problema ficará assim...
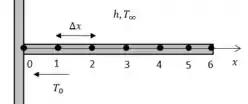
Logo, aplicando a formulação de diferenças finitas, podemos expressar uma equação geral para os nós interiores 1, 2, 3, 4 e 5:
Podemos simplifica-la, dividindo cada termo por . Portanto nossa equação se torna:
Passo 2
Agora podemos ter uma equação para cada nó.
Para o :
Para o :
Para o :
Para o :
Para o :
Para o :
Onde temos que...
Passo 3
Resolvendo as equações encontradas simultaneamente, chegamos nas temperaturas:
Passo 4
Para encontrarmos a taxa de transferência de calor de uma única aleta, precisamos apenas realizar o somatório do calor transferido de cada ponto nodal.
Para fazermos isso basta utilizarmos a equação abaixo:
Passo 5
Isso aí, agora que temos nossa taxa de transferência de calor para uma única aleta, precisamos encontrar o número de aletas para termos o valor total.
Pode ficar tranquilo, essa formula irá te ajudar...
Passo 6
Certo!! Agora podemos calcular a taxa de transferência de calor total.
Porém precisamos nos atentar a área exposta de transferência de calor que a área que está presente a cada espaçamento.
Portanto...
Resposta
Ei, a resposta está no passo a passo :)