Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 14.Problemas - Ex. 89

Um tanque com casca de 2 cm de espessura contém gás hidrogênio em condições atmosféricas de 25°C e 90 kPa. A válvula da carga do tanque tem diâmetro interno de 3 cm e estende-se a 8 m acima do tanque. Considerando que a tampa do tanque é deixada aberta para que o hidrogênio e o ar possam sofrer contradifusão equimolar por meio da passagem de 10 cm de comprimento, determine a vazão mássica de hidrogênio que se perde para a atmosfera através da válvula na fase inicial do processo.

Passo 1

Nossa situação é a seguinte:

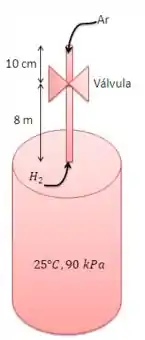
Temos um tanque com gás hidrogênio a T = 25 ° C = 298   K e P = 90   k P a . Acima do tanque temos uma tubulação de 8 m de comprimento e 3 cm de diâmetro, e ao final dela, uma válvula. Após a válvula há um tubo de 10 cm de comprimento aberto para a atmosfera. Ao abrir a válvula o hidrogênio começa a sair e ar começa a entrar no tanque, em um processo de contradifusão equimolar ( N A = - N B ). Devemos determinar a vazão mássica de gás hidrogênio que está saindo. Vamos lá???

Passo 2

Nosso primeiro passo é determinar onde ocorre o processo de transferência de massa. O nosso composto A (gás hidrogênio) parte da entrada do tubo, que vamos chamar de altura z = 0 . Neste ponto só há gás hidrogênio, então y A , 0 = 1 . Tudo bem?

O ar está entrando pelo topo da tubulação, na altura z = L = 8,1   m . Nesta altura só temos ar, então y A , L = 0 .

Nosso próximo passo é o cálculo do fluxo molar. Para um processo de contradifusão equimolar:

N A = D A B C L ( y A , 0 - y A , L )

Precisamos então da difusividade e da concentração molar do sistema. A difusividade do gás hidrogênio em ar é D A B = 7,2 x 10 - 5   m 2 / s para T = 298   K e P = 1   a t m = 101,3   k P a . Para obter a difusividade nas nossas condições podemos usar a relação:

D A B 1 D A B 2 = P 2 P 1 T 1 T 2 3 2

D A B 2 = D A B 1 P 1 P 2   T 2 T 1 3 2

D A B 2 = 7,2 x 10 - 5 x 101,3 9 0 x   298 298 3 2

D A B 2 = 8,104 x 10 - 5   m 2 / s

A concentração molar para uma mistura gasosa é dada por:

C = P R T

C = 9 0.000 8.314 x 298

C = 0,0 363   k m o l / m 3

Passo 3

O fluxo molar então é:

N A = D A B C L ( y A , 0 - y A , L )

N A = 8,104 x 10 - 5 x 0,0 363 8,1 x ( 1 - 0 )

N A = 3 , 63 x 10 - 7   k m o l / m 2 s

Para transformar o fluxo em taxa molar basta multiplicar pela área do tubo:

N A ˙ = N A x A

N A ˙ = N A x π D 2 4

N A ˙ = 3,63 x 10 - 7 x π x 3 x 10 - 2 2 4

N A ˙ = 2,57 x 10 - 1 0   k m o l / s

Nosso próximo passo é transformar a taxa molar N A ˙ em taxa mássica. Para isso precisamos da massa molar do gás hidrogênio:

M A = 2   k g / k m o l

A taxa mássica é dada por:

m ˙ = M x N ˙

Então:

m A ˙ = M A x N ˙ A

m ˙ A = 2 x 2,57 x 10 - 10

m ˙ A = 5,14 x 10 - 10   k g / s

Resposta

A taxa de hidrogênio que se perde para a atmosfera é de m ˙ A = 5,14 x 10 - 10   k g / s .

Ver Outros Exercícios desse livro