Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 175

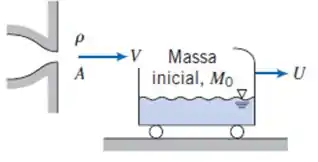
O tanque móvel mostrado pode movimentar ao longo de uma pista horizontal com resistência desprezível. Ele deve ser acelerado do repouso por um jato líquido que se choca contra sua parede curva e é defletido para dentro do tanque. A massa inicial do tanque é m 0 . Aplique as equações da continuidade e da quantidade de movimento para mostrar que, em qualquer instante, a massa do veículo mais a do líquido no seu interior é m = m o v / ( v - u ) . Obtenha uma expressão geral para u / v como uma função do tempo.

Passo 1

Considerações Iniciais:

  1. Escoamento em estado estacionário;
  2. Escoamento incompressível;
  3. Escoamento com velocidade constante ( V = v - u ) ;
  4. Escoamento uniforme;
  5. Força de corpo desprezível;
  6. Força de resistência desprezível.

Passo 2

Pelas considerações feitas no passo 1, utilizaremos a seguinte equação da quantidade de movimento:

F = F S + F B - ∫ V C a r ρ d ∀ = ∂ ∂ t ∫ V C V ρ   d ∀ + ∫ S C V ( ρ V ) d A = 0

Como estamos analisando um sistema x , temos:

F S x + F B x - ∫ V C a r x ρ d ∀ = ∂ ∂ t ∫ V C u ρ   d ∀ + ∫ S C u ( ρ V ) d A

Não há resistência ne força de campo, então, F S x = F B x = 0 :

- ∫ V C a r x ρ d ∀ = ∂ ∂ t ∫ V C u ρ   d ∀ + ∫ S C u ( ρ V ) d A

Não temos a variação das propriedades com o tempo, então:

∂ ∂ t = 0

Assim:

- ∫ V C a r x ρ d ∀ = ∫ S C u ( ρ V ) d A

Então:

- a r x ⋅ m = u 1 - ρ V A

Sendo:

u 1 = v - u .

Temos:

- a r x ⋅ m = v - u ⋅ [ ρ v - u A ]

Passo 3

Aplicando as equações da continuidade e da quantidade de movimento para mostrar que, em qualquer instante, a massa do veículo mais a do líquido no seu interior é m = m o v / ( v - u ) .

Temos que a r x = d u d t e ρ ( v - u ) A = d m d t , assim:

- m d u d t = ( v - u ) d m d t

m d u d t + ( v - u ) d m d t = 0

( v - u ) m = c o n s t a n t e

( v - u ) m = v m 0

m = v m 0 ( v - u )

Passo 4

Obtendo uma expressão geral para u / u 0 com uma função do tempo.

- m d u d t = v - u ⋅ ρ v - u A

Sendo m = v m 0 v - u :

- v m 0 ( v - u ) d u d t = v - u 2 ρ A

d u d t = - v - u 3 ρ A v m 0

d u v - u 3 = - ρ A v m 0 d t

∫ v v - u d u v - u 3 = - ρ A v m 0 ∫ 0 t d t

Integrando:

- 1 2 1 v - u 2 - 1 v 2 = - ρ A v m 0 t

1 ( v - u ) 2 - 1 v 2 = 2 ρ A t v m 0

Rearranjando:

( v - u ) 2 = v 2 + v m 0 2 ρ A t

( v - u ) 2 = v 2 1 + m 0 2 v ρ A t

v - u = v 1 + m 0 2 v ρ A t

u = v - v 1 + m 0 2 v ρ A t

u = v 1 - 1 + m 0 2 u 0 ρ A t

u v = 1 - 1 + m 0 2 u 0 ρ A t

Resposta

m = v m 0 v - u

u v = 1 - 1 + m 0 2 u 0 ρ A t

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na aplicação da equação do momento, explique por que em geral podemos desprezar a pressão atmosférica e trabalhar apenas com pressões manométricas.
Considere dois corpos rígidos com mesma massa e velocidade angular. Você acha que esses dois corpos devem ter o mesmo momento angular? Explique.
Descreva as forças de corpo e as forças de superfície e explique como a força resultante que age sobre o volume de controle é determinada. O peso do fluido é uma força de corpo ou uma força de superfí
Em determinado local, um helicóptero exige mais energia no verão ou no inverno para atingir um desempenho especificado? Explique.
Para flutuar no alto de uma montanha, um helicóptero precisa de mais, menos ou da mesma potência que precisaria para flutuar no nível do mar? Explique.