Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 84

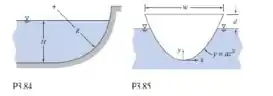
Uma superfície submersa curva, no formato de um quarto de cilindro com raio   R   =   0,3   m está mostrada na figura. A forma pode resistir a uma carga máxima vertical de 1,6   k N antes de se romper. A largura é w   =   1,25   m Determine a profundidade máxima H para a qual a configuração pode ser mantida. Determine a linha de ação da força vertical para esta condição. Trace um gráfico dos resultados em função da profundidade da faixa de concreto 0   ≤   H   ≤   R .

Passo 1

Nessa questão temos uma superfície curva, com raio R e largura w , em que há uma substância (concreto líquido) na profundidade H . Devemos encontrar a profundidade máxima do concreto para evitar rachaduras, a linha de ação no formulário, e, por fim, traçar a força vertical e a linha de ação sobre H, variando de 0 a R .

Agora vamos ver com quais expressões podemos calcular isso:

d p d h = ρ g , pressão hidrostática onde h é positivo para baixo.

F v = ∫ p d A y , força hidrostática vertical

x ' F V = ∫ x d F V

Como todo problema da MecFLu, fazemos algumas considerações: fluido estático e incompressível; pressão atmosférica atuando na superfície.

Passo 2

Vamos começar integrando a equação da pressão hidrostática. A partir da geometria, temos: y = R sin ⁡ θ , x = R cos ⁡ θ , h = y - d , d = R - H e d A = w R   d θ .

Assim, podemos aplicar na equação:

F v = ∫ p d A y

F v = ∫ θ 1 π 2 ρ g   R sin ⁡ θ - d sin ⁡ θ w R   d θ

Onde θ 1 = asin ⁡ d R .

F v = ρ g w R ∫ θ 1 π 2 [ R sin ⁡ θ 2 - d sin ⁡ θ ]   d θ

Substituindo os valores temos:

F V = ρ g w R R × π 4 - θ 1 2 + sin ⁡ 2 θ 4 - d ( cos ⁡ θ 1 )

Definimos os valores para as funções trigonométricas:

sin ⁡ θ 1 = R - H R

cos ⁡ θ 1 = R 2 - R - H 2 R = 2 R H - H 2 R

sin ⁡ 2 θ 1 = 2 sin ⁡ θ 1 cos ⁡ θ 1 = 2 ( R - H ) 2 R H - H 2 R 2

Substituindo na expressão que formamos da força:

F V = ρ g w R R π 4 - acos ⁡ 1 - H R 2 + 2 R - H 2 R H - H 2 2 R 2 - d ( 2 R H - H 2 R )

Assim, resolvemos essa equação para encontrar H :

H = 0,237   m

Passo 3

Para achar a linha de ação, temos:

x ' F V = ∫ x ρ g h sin ⁡ θ d A

x ' F V = ρ g R 2 w ∫ θ 1 π 2 [ R sin ⁡ θ 2 cos ⁡ θ - d sin ⁡ θ cos ⁡ θ ]   d θ

Avaliando a integral:

x ' F V = ρ g R 2 w R 3 1 - sin ⁡ θ 1 3 - d 2 × cos ⁡ θ 1 2

Assim, podemos encontrar por:

x ' = x ' F V F v = ρ g R 2 w F v R 3 1 - sin ⁡ θ 1 3 - d 2 × cos ⁡ θ 1 2

Definimos os valores para as funções trigonométricas:

sin ⁡ θ 1 = 0,3 - 0,237 0,3 = 0,21

cos ⁡ θ 1 = 0,3 - 0,21 2 = 0,51

Então,

x ' = 2,5 × 999 × 9,81 × 0,3 2 × 0,51 × 1 1,6 × 10 3 [ 0,3 m 3 × [ 1 - 0,21 3 ] - 0,21 2   - 1,24 2 ]

x ' = 0,703 [ 0,3 m 3 × [ 1 - 0,21 3 ] - 0,21 2   - 0,51 2 ]

x ' = 0,363   m

Prontinho!!

Passo 4

Para a força vertical e a linha de ação sobre H, respectivamente, variando de 0 a R , temos:

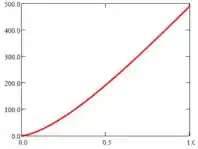
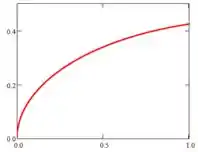
Prontinho!!

Resposta

H = 0,237   m

x ' = 0,363   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma esfera de raio R está parcialmente imersa, a uma profundidade d, em um líquido com densidade relativa SG. Obtenha uma expressão algébrica para a força de empuxo atuando sobre a esfera como uma fun
Uma canoa é representada por um semicilindro circular reto, com R = 0,35m e L = 5,25m . A canoa flutua sozinha em água com seu fundo a uma profundidade d = 0,245m . Estabeleça uma expressão algébrica
Uma tora cilíndrica, com D = 0,3 m e L = 4 m, é mais pesada na sua extremidade inferior, de modo que flutua verticalmente com 3 m submersos na água. Quando deslocada verticalmente da sua posição de eq
Determine o peso específico da esfera mostrada na figura, se o seu volume é de 0,025m 3 . Enuncie todas as considerações feitas. Qual será a posição de equilíbrio da esfera, se o peso for removido?
O cilindro mostrado é suportado por um líquido incompressível de massa específica ρ , e é articulado ao longo do seu comprimento. O cilindro, de massa M , comprimento L e raio R , está imerso no líqui