Testes são realizados em um modelo de embarcação com 1 m de comprimento em um tanque de água. Os resultados obtidos (após a realização de análise de dados) são os seguintes:

A consideração é de que a modelagem do arrasto de onda é feita usando o número de Froude, e o arrasto pelo atrito pelo número de Reynolds. A embarcação em tamanho normal terá 50 m de comprimento quando construída. Estime o arrasto total quando esta embarcação está navegando a 7,7 m/s e a 10,3 m/s, em um lago de água doce.

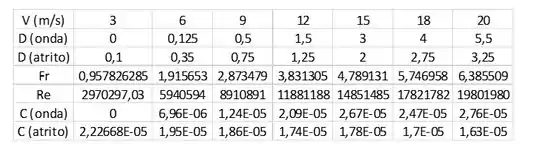
Agora vamos analisar os dados fornecidos para o modelo, então, utilizando as fórmulas descritas no passo 1, conseguimos chegar nos seguintes resultados:

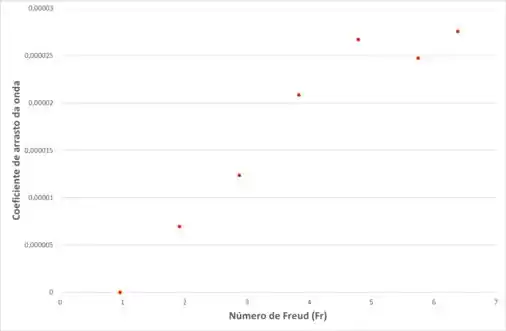
E, o gráfico que representa o coeficiente de arrasto da onda em função do número de Freud será:

E, aquele que representa o coeficiente de arrasto de atrito em função do número de Freud será:

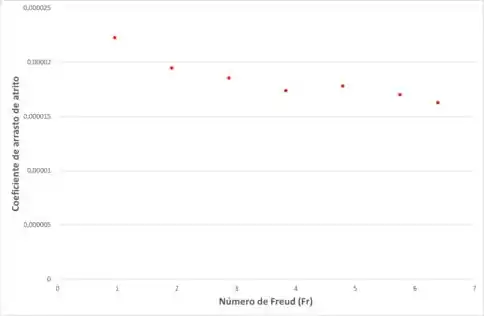
Então, podemos perceber que o coeficiente de arrasto da onda tem um comportamento praticamente linear com o número de Freud. Já o coeficiente de atrito aparenta ser um valor constante.

Agora, para a embarcação real, temos as seguintes condições:

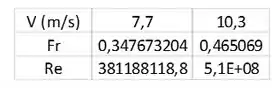
Então, podemos ver que para a embarcação real, temos um número de Freud baixo e um Reynolds alto. Dessa forma, podemos utilizar as relações obtidas no passo 2, dessa forma, teremos:

Esses valores serão os mesmos para as duas velocidades, já que isso não altera significativamente o Reynolds e nem o número de Freud para alterar os coeficientes de atrito. Então, para temos:

Substituindo os valores conhecidos, temos:

E, para a força de atrito, temos:

Substituindo os valores conhecidos, temos:

Então, a força total nessa condição será:

Agora para a velocidade de , temos:

Substituindo os valores conhecidos, temos:

E, para a força de atrito, temos:

Substituindo os valores conhecidos, temos:

Então, a força total nessa condição será: