Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 11.Problemas - Ex. 119

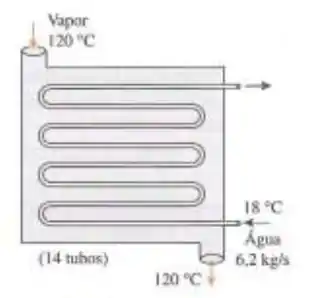
Um trocador de calor de casco e tubo com 1 passe no casco e 14 passes no tubo é utilizado para aquecer água nos tubos com condensação de vapor geotérmico a 120°C h f g = 2203 k J k g no lado do casco. Os tubos têm parede fina, diâmetro de 2,4 cm e 3,2 m de comprimento por passe. A água c p =   4180 J k g K entra nos tubos a 18°C a uma taxa de 6,2 kg/s. Considerando que a diferença de temperatura entre os dois fluidos na saída é 46°C, determine (a) a taxa de transferência de calor, (b) a taxa de condensação do vapor e (c) o coeficiente global de transferência de calor.

Passo 1

Bora começar mais uma galerinhaa!!

Bom, sabemos que a água esta sendo aquecida pelo vapor, certo?

Então nós podemos calcular a taxa de transferência de calor usando a equação:

Q ˙ = m f ˙ c p ,   f ( T f ,   s a i - T f ,   e n t r a )

Já sabemos que:

m f ˙ = 6,2 k g s

c p ,   f = 4180 J k g K

T f ,   e n t r a = 18 ° C

T q ,   s a i - T f ,   s a i = 46 ° C

Se:

T q ,   s a i = 120 ° C

Então:

120 ° C - T f ,   s a i = 46 ° C →   T f ,   s a i = 74 ° C

Substituindo:

Q ˙ = 6,2 k g s 4180 J k g K ( 74 ° C - 18 ° C )

Q ˙ = 1451296   W

Ou melhor:

Q ˙ = 1451 , 296   k W

É isso aí!!

Achamos a letra (a), bora pra (b)??

Passo 2

Na letra (b) queremos achar a taxa de condensação do vapor, ok?

Sendo assim nós podemos usar a fórmula:

Q ˙ = m ˙ h f g

Isolando:

m ˙ = Q ˙ h f g

E sabendo que:

Q ˙ = 1451 , 296   k W

h f g = 2203 k J k g

Então:

m ˙ = 1451,296   k W 2203 k J k g

m ˙ = 0,658 k g s

Preparados para a (c)??

Passo 3

Na letra (c) nós precisamos calcular o coeficiente global de transferência de calor. Para isso nós podemos usar a equação:

Q ˙ = U F A s ∆ T l m

No caso de condensador:

F = 1

E já estamos carecas de saber que:

Q ˙ = 1451,296   k W

Mas ainda precisamos calcular a diferença média logarítima e a área, certo?

Usando a fórmula:

∆ T l m = ∆ T 1 - ∆ T 2 ln ⁡ ∆ T 1 ∆ T 2

Lembrando que:

∆ T 1 = T q ,   e n t r a - T f ,   s a i

∆ T 2 = T q ,     s a i - T f ,   e n t r a

Nós temos quase tudo:

T q ,   e n t r a = T q ,     s a i = 120 ° C

T f ,   e n t r a = 18 ° C

T f ,   s a i = 74 ° C

Substituindo::

∆ T 1 = 120 ° C - 74 ° C = 46 ° C

∆ T 2 = 120 ° C - 18 ° C = 102 ° C

Calculando a diferença:

∆ T l m = 46 ° C - 102 ° C ln ⁡ 46 ° C 102 ° C

∆ T l m = 70,32 ° C

Passo 4

Agora só falta calcularmos a área, não é?

Se lembram como?

A s = n π D L

Lembrando que:

n = 14   t u b o s  

D = 2,4   c m = 0,024   m

L = 3,2   m

Substituindo:

A s = 14 π 0,024   m 3,2   m

A s = 3,3 78   m ²

Belezinhaa!!

Agora é só colocar na fórmula do Passo 3:

1451,296   k W = U 1 3,378   m 2 70,32 ° C

U = 6,11 k W m 2 . ° C

Gostaram?

Resposta

  1. Q ˙ = 1451,296   k W ;
  2. m ˙ = 0,658 k g s ;
  3. U = 6,11 k W m 2 . ° C .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

37 - Para determinadas temperaturas de entrada e de saída, para que tipo de trocador de calor Δ t l m vai ser maior: trocador de calor de tubo duplo de escoamento paralelos, tubo duplo contracorrente,
31 - Como a diferença de temperatura média logarítmica de um trocador de calor difere da diferença de temperatura média aritmética?No caso de temperaturas de entrada e saída especificadas, qual dessas
47 - Um trocador de calor de escoamento paralelo de tubo duplo é usado para aquecer a água fria da torneira com água quente.A água quente c p = 4,25 k J k g ⋅ K entra no tubo a 85° C a uma taxa de 1,4
41 – Um teste é realizado para determinar o coeficiente global de transferência de calor em um trocador de calor de casco e tubos para óleo-água que tem 24 tubos em diâmetro interno de 1,2c m e 2m de
30 - Na relação de transferência de calor Q ˙ = U A s ∆ T l m para um trocador de calor, como échamado ∆ T l m ?Como ela é calculada para um trocador de calor de escoamento paralelo e uma contracorren