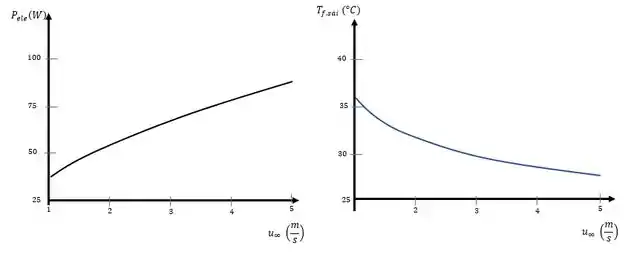
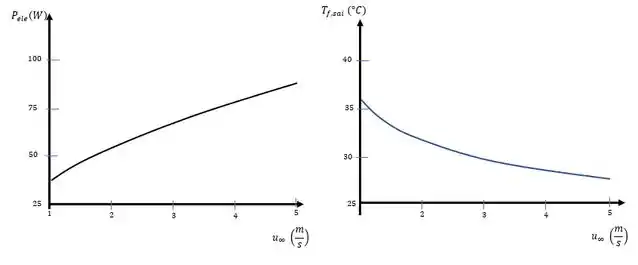
O dissipador de calor do Problema tem sua utilização cogitada em uma aplicação na qual a dissipação de potência é de somente e o engenheiro propõe o uso no resfriamento de ar a . Levando em conta o aumento da temperatura do ar ao longo de seu escoamento através do dissipador de calor, represente graficamente a dissipação de potência permitida e a temperatura de saída do ar como funções da velocidade do ar, na faixa , com a restrição de que a temperatura da base não exceda . As propriedades do ar podem ser aproximadas por e . Sugestão: Suponha que o ar não escape pela superfície superior do dissipador de calor, use uma correlação para escoamento interno e veja o Problema .

Vamos lá! Os dados são dados na questão então não precisamos nos preocupar com tabela nessa questão \o/.

Vamos organizar uma série de equações para podermos analisar nosso problema graficamente, cada série tá definida por passo.

Pela consideração temos que o número de é dado por:

Lembrando que é a tangente hiperbólica:

Para:

Onde é a área de cada coluna do dissipador e seu perímetro, da eficiência convectiva temos:

Agora temos que a resistência térmica total é dada por:

é o número de passagens de ar é a área da fresta por onde o ar passa, é a área total.

Para calcularmos a eficiência da fresta precisamos calcular o seu parâmetro , que é dado por:

Assim temos:

Questão longa né, daquele tipo que quando você pensa!

Mas não vamos perder o foco! Já chegamos na metade do caminho!

Temos que o nosso coeficiente calorifico para o fluído mínimo é dado por:

A eficiência por sua vez é dada por:

Agora calculando taxa de transferência de calor:

Por fim a temperatura de saída é dada por:

Kkk, memes a parte vamos matar essa questão de vez!

Usando um software podemos resolver as equações a para a velocidade do ar que passa pelo nosso dissipador, substituindo os dados numéricos que a questão.

Resolvendo para a e em função de temos:

Isso é tudo pessoal! \o/