Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 11.Problemas - Ex. 53

Um trocador de calor casco e tubos tem 135 tubos com paredes delgadas em uma configuração com dois passes, cada um com 12,5   m m de diâmetro e uma área superficial total de 47,5   m 2 . Água (o fluido que passa pelo lado dos tubos) entra no trocador de calor a 15 ° C e 6,5   k g / s , sendo aquecida por gases de exaustão que entram a 200 ° C e 5   k g / s . Considere que o gás tinha as propriedades do ar atmosférico e o coeficiente global de transferência de calor seja de aproximadamente 200   W / ( m 2 · K ) .

(a) Quais são as temperaturas de saída do gás e da água?

(b) Admitindo escoamento plenamente desenvolvido, qual é o valor do coeficiente de transferência de calor por convecção no lado dos tubos?

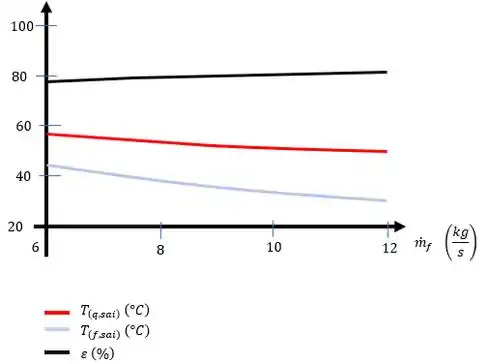
(c) Com todas as demais condições permanecendo sem alteração, represente graficamente a efetividade e as temperaturas de saída dos fluidos como funções da vazão mássica da água na faixa de 6 a 12   k g / s .

(d) Qual é a temperatura de entrada do gás necessária para que o trocador de calor forneça 10   k g / s de água quente a uma temperatura de saída de 42 ° C , com todas as demais condições permanecendo inalteradas? Qual é a efetividade para essa condição de operação?

Passo 1

Vamos lá!! Nosso problema se trata de um sistema simples de trocador de calor tendo isso em mente vamos ilustrar isso com nosso esqueminha pra facilitar o entendimento do problema.

Sendo o nosso tubo está enrolado e tem duas voltas.

Agora precisamos fazer nossas famosas considerações. Hehe (u.u)

I - O   g á s   t e m   a s   m e s m a s   p r o p r i e d a d e s   d o   a r

I I - T r o c a   d e   c a l o r   c o m   a   v i z i n h a n ç a   d e s p r e z í v e l

I I I - E s c o a m e n t o   d e n t r o   d o   t u b o   é   c o m p l e t a m e n t e   d e s e n v o l v i d o

I V - O   c o e f i c i e n t e   c o n v e c t i v o   m é d i o   é   c o n s t a n t e   d u r a n t e   o   p r o c e s s o

Passo 2

(a)

Vamos lá! Vamos usar os dados da tabela A - 6 para a água à 300   K e A - 4 para o ar.

Agora precisamos calcular as temperaturas, mas primeiro vamos calcular nosso coeficiente calorifico para encontrarmos a temperatura pelo método ε - N T U , assim temos:

C f = m ˙ f ⋅ c p ,   f = 6 , 5 k g s ⋅ 4179 J k g ⋅ K = 27 . 164   W K

C q = m ˙ q ⋅ c p ,   q = 5 , 0 k g s ⋅ 1014 J k g ⋅ K = 5 . 070   W K

Como C f = C m a x e C q = C m i n , temos que C r = C q / C f = 0,19 .

Do nosso coeficiente N T U , para C m i n = C f , temos:

N T U = U ⋅ A C m i n = 200   W m 2 ⋅ K ⋅ 47,5   m 2 5.070   W K

N T U = 1,87

Usando a figura 11.12 para C r = 0,19 e N T U = 1,87 , temos que ε ≈ 0,78 .

Agora podemos calcular a temperatura de saída dos gases, da relação da eficiência temos:

ε = q q m a x = C q T q ,   e n t - T q ,   s a i C m i n T q ,   e n t - T f , e n t , 200   ° C - T q ,   s a i 200   ° C - 15   ° C = 0,78

T q ,   s a i = 55,7   ° C

Do balanço de energia para os dois fluídos temos:

C q T q ,   e n t - T q ,   s a i = C f T f ,   e n t - T f ,   s a i

Dividindo ambos os lados por C f

C r T q ,   e n t - T q ,   s a i = T f ,   e n t - T f ,   s a i

0,19 200   ° C - 55,7   ° C = 15   ° C - T f ,   s a i

T f ,   s a i = 41,9   ° C

Passo 3

(b)

Vamos matar essa?!

Pra calcularmos o coeficiente convectivo vamos analisar o escoamento, calculando o número de Reynolds temos:

R e = 4 m ˙ N π D μ = 4 ⋅ 6,5 135 ⋅ π ⋅ 12,5 ⋅ 10 - 3   m ⋅ 855 ⋅ 10 - 6   N s ⋅ m 2

R e = 5.736

Para o escoamento totalmente desenvolvido e não turbulento pois R e < 10.000 , a relação de D i t t u s - B o e l t e r não é estritamente aplicável, mas nos permite ter uma estimativa, assim temos:

N u - = h - D k = 0,023 R e 4 5 ⋅ P r 0,4 = 0,023 5.736 4 5 ⋅ 5,83 0,4 = 47,3

h - = N u - ⋅ k D

h - = 2320   W m 2 ⋅ K

Passo 4

(c)

Se refizermos o Passo 2 variando a vazão mássica da água vamos ter um arranjo de temperatura.

Recomendo inserirmos as equações em um software de sua preferência com um laço de repetição, após isso realizarmos o plot do gráfico.

A vazão mássica da água varia num intervalo de:

6 ≤ m ˙ f ≤ 12     k g s

Assim temos:

Passo 5

(d)

Reutilizando as equações do Passo 2 :

C f = m ˙ f ⋅ c p ,   f

C q = m ˙ q ⋅ c p ,   q

ε = q q m a x = C q T q ,   e n t - T q ,   s a i C m i n T q ,   e n t - T f , e n t

C r T q ,   e n t - T q ,   s a i = T f ,   e n t - T f ,   s a i

Se vaiarmos a vazão da água quente m ˙ q mantendo a temperatura de saída T f ,   s a i = 42 ° C mantendo todos os demais dados constantes temos:

T h ,   e n t = 74,4   ° C

ε = 0,55

Isso é tudo pessoal!

Resposta

(a) T q ,   s a i = 55,7   ° C ,   T f ,   s a i = 41,9   ° C

(b) h - = 2320   W m 2 ⋅ K

(c) Gráfico vide passo a passo

(d) T h ,   e n t = 74,4   ° C , ε = 0,55

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Óleo quente ( c p = 2200J / k g · K ) deve ser resfriado por água ( c p = 4180J / k g · K ) em um trocador de calor casco e com 2 passa no casco e 12 tubos.Os tubos são de cobre, de paredes finas, com
Água ( c p = 4180J / k g · K ) entra nos tubos de 2,5c m de diâmetro interno de um trocador de calor de tubo duplo em contracorrente a 20 ℃ ℃ a uma taxa de 2,2k g / s .A água é aquecida pela condensaç
Etanol é vaporizado a 78 ℃ ℃ ( h f g = 846k J / k g ) em um trocador de calor de tubo duplo de escoamento paralelo a uma taxa de 0,04k g / s por óleo quente ( c p = 2200J / k g ∙ K ) que entra a 115 ℃
Em um trocador de calor de escoamento paralelo, o N T U é calculado em 2,5 .A efetividade mais baixa possível para este trocador de calor éa) 10%b) 27%c) 41%d) 50%e) 92%
Vapor deve ser condensado no lado do casco de um condensador com 2 passes no casco e 8 passes no tubo, com 20 tubos em cada passe.A água de resfriamento entra nos tubos a uma taxa de 2k g / s .Se a ár