Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 11.Problemas - Ex. 52
Um sistema de armazenamento de energia é proposto para absorver energia térmica coletada durante o dia por um coletor solar e liberá-la durante a noite para aquecer uma edificação. O componente-chave do sistema é um trocador de calor casco e tubos com o lado do casco cheio de (veja o Problema ).
(a) Água quente vinda do coletor solar é enviada ao trocador de calor a e , passando por dentro dos tubos do feixe tubular que tem tubos, dois passes nos tubos e um comprimento dos tubos por passe de . Os tubos metálicos, de paredes delgadas, têm diâmetro . No fundido há convecção natural, fornecendo um coeficiente de transferência de calor médio de no lado externo de cada tubo. Determine o volume de que é fundido em um período de . Se o volume total de deve ser superior ao volume fundido em , determine o diâmetro do casco que tem comprimento igual a .
(b) Durante a noite, água a é passada pelo trocador de calor, elevando sua temperatura e solidificando o . Você espera que a taxa de transferência de calor seja igual, maior ou menor do que a taxa de transferência de calor na parte (a)? Apresente sua argumentação.
Passo 1
Vamos lá!!
Antes de mais nada, o é apenas uma cadeia de hidrocarbonetos, na questão ele funciona como um catalizador pra troca de calor do calor, como o ilustrado.
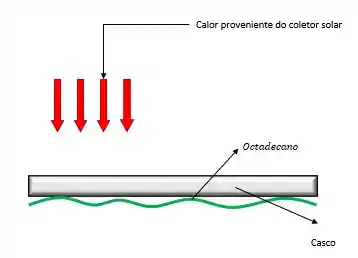
Tendo isso em mente vamos ilustrar isso com nosso esqueminha pra facilitar o entendimento do problema.
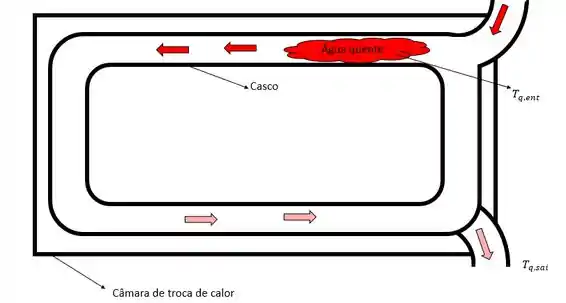
Sendo o nosso tubo está enrolado e tem duas voltas.
Agora precisamos fazer nossas famosas considerações. Hehe (u.u)
Passo 2
(a)
Vamos lá! Os dados do são dados no problema , vamos usar também os dados da tabela para a água à .
Agora precisamos calcular o diâmetro para as condições desejadas, mas primeiro vamos calcular nosso coeficiente calorifico, assim temos:
Do nosso coeficiente NTU, para , temos:
Onde:
Sendo o número de tubos , para duas voltas temos:
Substituindo temos que
Da relação da eficiência temos:
Temos que a transferência de calor é dada por:
Sendo a temperatura de fusão do , substituindo temos.
Agora podemos calcular o volume de material fundido após as horas, assim temos:
Como o volume deve ser superior ao nosso assim temos:
Pra matarmos essa de vez temos que o volume do tubo é dado por:
Como, assim finalmente podemos calcular o diâmetro do casco que é dado por:
Passo 3
(b)
Vamos matar essa?!
Tanto para o processo de solidificação tanto para o processo de fusão do temos que a variação de temperatura do processo em relação a temperatura da água é praticamente a mesma com valor:
Entretanto, para o processo de solidificação o coeficiente condutivo é:
Que é um valor muito baixo, logo a resistência térmica será alta, como consequência a taxa de transferência de calor será menor do que para o processo de fusão!
Isso é tudo pessoal!
Resposta
(a)
(b) Será menor!