Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 11.Problemas - Ex. 88

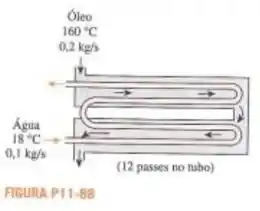
Óleo quente ( c p = 2200   J / k g · K ) deve ser resfriado por água ( c p = 4180   J / k g · K ) em um trocador de calor casco e com 2 passa no casco e 12 tubos. Os tubos são de cobre, de paredes finas, com diâmetro de 1,8   c m . O comprimento de cada passe de tubo no trocador de calor é de 3   m , e o coeficiente global de transferência de calor é 340   W / m 2 · K . A água escoa através dos tubos a uma taxa total de 0,1   k g / s , e o óleo escoa através da casco a uma taxa de 0,2   k g / s . A água e o óleo entram com temperaturas de 18 ℃ e 160 ℃ , respectivamente. Determine a taxa de transferência de calor no trocador de calor e as temperaturas de saída da água e do óleo. 

Respostas:  36,2   k W , 104,6 ℃ , 77,7 ℃

Passo 1

Dados fornecidos:

Tipo: passes de 2 conchas e 12 passes de tubo

Diâmetro de tubos de paredes finas:  D = 1,8   c m = 0,018   m

Comprimento dos tubos de parede fina: L = 3   m

Coeficiente global de transferência de calor: U = 340   W / m 2 · K

Calor específico de óleo quente: c p h = 2200   J / k g · K

Vazão mássica do óleo quente: m ˙ h = 0,2   k g / s

Temperatura de entrada de óleo quente: T h , e n t r a d a = 160 ℃

Calor específico da água: c p c = 4180   J / k g · K

Vazão mássica da água: m ˙ c = 0,1   k g / s

Temperatura de entrada de água: T c , e n t r a d a = 18 ℃

Premissas:

1) Existem condições operacionais estáveis.

2) O trocador de calor é bem isolado, de modo que a perda de calor para o ambiente é insignificante e, portanto, a transferência de calor do fluido quente é igual à transferência de calor para o fluido frio.

3) Alterações nas energias cinética e potencial das correntes de fluido são desprezíveis.

4) A espessura do tubo é insignificante, pois possui paredes finas.

5) O coeficiente global de transferência de calor é constante e uniforme.

Passo 2

Fala galera!!!

Para resolver essa questão, temos que calcular as taxas de capacidade térmica dos fluidos quente e frio. Para o fluido quente (óleo), temos:

C h = m ˙ h c p h = 0,2   k g / s × 2200   J / k g · K = 4 40   W / K

Para o fluido frio (água), temos:

C c = m ˙ c c p c = 0,1   k g / s × 4180   J / k g · K = 418   W / K

Portanto, a menor das duas taxas de capacidade térmica é:

C m i n = C c = 418   W / K

Temos também que a relação das taxas de capacidade é a seguinte:

c = C m i n C m á x = 418   W / K 440   W / K = 0,95

Passo 3

Fluidos com menor valor de taxa de capacidade experimentam a maior mudança de temperatura, de modo que a taxa máxima de transferência de calor se torna a seguinte:

Q ˙ m á x = C m i n T h , e n t r a - T c , e n t r a

Substituindo os termos da equação acima pelos dados obtidos, temos:

Q ˙ m á x = 418   W / K 160 ℃ - 18 ℃

Q ˙ m á x = 59356   W

Passo 4

Agora, vamos calcular o N T U para este trocador de calor. Assim temos

N T U = U A s C m i n

Aqui, U é o coeficiente global de transferência de calor e A s é a área da superfície de troca de calor que é n π D L .

N T U = U n π D L C m i n

Substituindo os termos da equação acima pelos dados obtidos, temos:

N T U = 340   W / m 2 · K 12 π 0,018   m 3   m 418   W / K

N T U = 1,656

Passo 5

Ao analisarmos a figura 11-26(d) podemos encontrar a efetividade para esse trocador de calor.

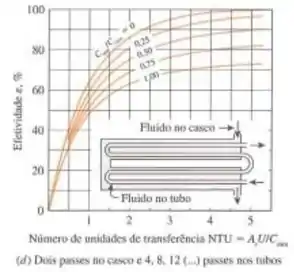
Para N T U = 1,656 e c = C m i n / C m á x = 0,95 , temos que e efetividade é:

ε = 0,61

Passo 6

Então a taxa real de transferência de calor pode ser determinada da seguinte maneira:

Q ˙ = ε × Q ˙ m á x

Substituindo pelos dados obtidos, temos:

Q ˙ = 0,61 × 59356   W

Q ˙ = 36207,16   W

Q ˙ = 36 , 2   k W

Portanto, a taxa de transferência de calor no trocador de calor é 36,2   k W .

Passo 7

Temos então, que a temperatura de saída da água pode ser calculada pela seguinte relação:

Q ˙ = C c T c , s a í d a - T c , e n t r a d a

T c , s a í d a = T c , e n t r a d a + Q ˙ C c

Substituindo os termos da equação pelos dados obtidos, temos:

T c , s a í d a = 18 ℃ + 36207,16   W 418   W / K

T c , s a í d a = 104,62 ℃

Portanto, a temperatura de saída do ar é  104 , 6 ℃ .

Passo 8

Então a temperatura de saída da água pode ser calculada pela seguinte relação:

Q ˙ = C h T h , e n t r a d a - T h , s a í d a

T h , s a í d a = T h , e n t r a d a - Q ˙ C h

Substituindo os termos da equação pelos dados obtidos, temos:

T h , s a í d a = 160 ℃ - 36207,16   W 440   W / K

T h , s a í d a = 77,71 ℃

Portanto, a temperatura de saída do ar é  77,7 ℃ .

Resposta

Q ˙ = 36,2   k W

T á g u a , s a í d a = 104,62 ℃

T ó l e o , s a í d a = 77,71 ℃

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A temperatura do fluido quente pode estar abaixo da temperatura de entrada do fluido frio em algum local do trocador de calor? Explique.
O radiador em um automóvel é um trocador de calor de escoamento cruzado ( U A s = 10k W / K ) que utiliza ar ( c p = 1,00k J / k g · K ) para resfriar o fluido de resfriamento do motor ( c p = 4,00k J
Óleo em um motor está sendo resfriado pelo ar em um trocador de calor com fluxo cruzado, no qual ambos os fluidos são misturados. O óleo c p q = 2047 J k g . K fluindo a uma taxa de escoamento de 0,02
Água fria c p = 4180 J k g . K conduzida a uma ducha entra em um trocador de calor de tubo duplo com parede fina em contracorrente a 15°C, a uma taxa de 0,25 kg/s, e é aquecido a 45°C com água quente
Um trocador de calor de casco e tubo com 2 passes no casco e 8 passes no tubo é usado para aquecer álcool etílico c p = 2670 J k g . ° C nos tubos de 25°C a 70°C a uma taxa de 2,1 kg/s. O aquecimento