2. Um tubo de aço inoxidável AISI 302, com diâmetros interno e externo de Di = 22 mm e De = 27 mm, respectivamente, é usado em um trocador de calor com escoamento cruzado. Os fatores de deposição, , nas superfícies interna e externa são estimados serem iguais a 0,0004 m2 · K/W e 0,0002 m2 · K/W, respectivamente.

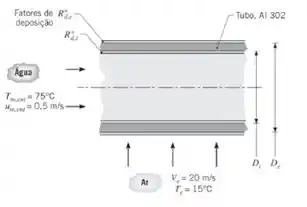
(a) Determine o coeficiente global de transferência de calor com base na área externa do tubo, Ue. Compare as resistências térmicas devido à convecção, à condução na parede do tubo e à deposição.

(b) Em vez de ar escoando sobre o tubo, considere uma situação na qual o fluido em escoamento cruzado é água a 15°C, com uma velocidade de Ve = 1 m/s. Determine o coeficiente global de transferência de calor com base na área externa do tubo, Ue. Compare as resistências térmicas devido à convecção, à condução na parede do tubo e à deposição.

(c) Para as condições água-ar da parte (a) e velocidades médias, um,ent, de 0,2; 0,5 e 1,0 m/s, represente graficamente o valor do coeficiente global de transferência de calor como uma função da velocidade do escoamento cruzado para 5 ≤ Ve ≤ 30 m/s.

(d) Para as condições água-água da parte (b) e velocidades do escoamento cruzado, Ve, de 1, 3 e 8 m/s, represente graficamente o valor do coeficiente global de transferência de calor como uma função da velocidade média para 0,5 ≤ um,ent ≤ 2,5 m/s.

Letra (a)

O Calculo do coeficiente geral com base na área externa do tubo para o tubo de aço inoxidável será dado pela seguinte expressão:

Para encontrar o coeficiente geral para o aço inoxidável do tipo 302, devemos pegar as propriedades do aço inoxidável das propriedades termofísicas da tabela A-1.

Pegue as propriedades do ar das propriedades termofísicas dos fluidos saturados da tabela A-4.

Com isso, devemos calcular a resistência condutora de transferência de calor do tubo.

Calcular a resistência à incrustação por transferência de calor do tubo na superfície interna

Calcular a resistência à incrustação por transferência de calor do tubo na superfície externa

Calcular a resistência convectiva à transferência de calor na superfície interna do tubo

Primeiro neste caso, devemos encontrar o número de Reynolds para o tubo horizontal para calcular o coeficiente de transferência de calor por convecção e então encontrar a resistência mostrada acima:

Portanto, para o número de tubos de Reynolds  , o fluxo é turbulento.

Use a equação do número de Nusselt para fluxo turbulento em cilindros horizontais para fluxo interno:

Estamos quase lá!!!

Calcular o coeficiente de transferência de calor por convecção na superfície interna usando o número de Nusselt

Agora que temos o valor de h em mãos, basta voltar na equação da resistencia para encontrar o valor da mesma:

Calcular a resistência convectiva à transferência de calor na superfície externa do tubo

Da mesma forma que anteriormente,

Portanto, para o número de tubos de Reynolds  , o fluxo é turbulento.

Use a equação do número de Nusselt para fluxo turbulento para alto número de Reynolds para fluxo externo sobre um cilindro.

Estamos quase lá!!!

Calcular o coeficiente de transferência de calor por convecção na superfície externa usando o número de Nusselt

Agora que temos o valor de h em mãos, basta voltar na equação da resistencia para encontrar o valor da mesma:

Substituindo todas essas resistencias calculadas na equação mais geral descrita no inicio do problema teremos:

Portanto, o coeficiente geral de transferência de calor com base na área externa é .