Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 7.Problemas - Ex. 81
Para as condições fornecidas no Problema 7.80, quais são a velocidade terminal e a altura do tanque se óleo de motor a for usado como refrigerante no lugar da água?
Passo 1
Essa questão faz referência ao Problema 7.80 onde temos o diâmetro das esferas de cobre que estão em banho de óleo. E temos também as temperaturas inicial e final.
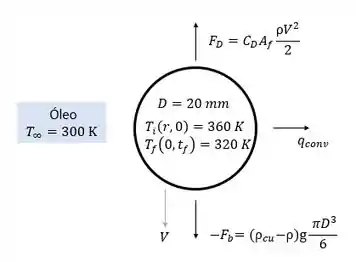
A partir disso queremos encontrar a velocidade terminal no banho e a altura do banho de óleo.
Passo 2
Para resolver essa questão vamos assumir que a esfera desce na velocidade terminal e a temperatura da superfície é uniforme, mas variável com o tempo. Além disso, as propriedades do cobre e do óleo foram retiradas da Tabela A.1.
Um balanço de forças realizado na esfera gera:
Substituindo os valores retirados da Tabela A.1, temos:
É necessária uma solução iterativa, na qual o é obtido da Figura 7.9 com,
A convergência é alcançada com,
Para essa velocidade temos que e
Passo 3
Usando a correlação de Whitaker:
Então,
Para determinar a aplicabilidade do método de capacitância concentrada, vamos analisar o número de Biot.
Portanto, o método de capacitância concentrada pode ser usado.
Passo 4
Assim, temos que:
Substituindo os valores encontramos,
Então, a altura do tanque requerida é: