Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 9.Problemas - Ex. 91
Uma cavidade retangular é formada por duas placas paralelas quadradas com 0,5 m de lado, separadas por uma distância de 50 mm. As fronteiras laterais da região entre as placas são isoladas. A placa aquecida é mantida a 325 K e a placa resfriada a 275 K. Estime o fluxo térmico entre as superfícies para três orientações da cavidade, usando a notação da Figura 9.6: vertical com τ = 90°, horizontal com τ = 0° e horizontal com τ = 180°.
Passo 1
Vamo analisar o enunciado junto pra entender o que ele quer de você.
Temos uma cavidade retangular é formada por duas placas paralelas quadradas com , com temperaturas de, respectivamente, e , como demonstra o esquema ilustrativo abaixo com algumas grandezas que vamos utilizar:
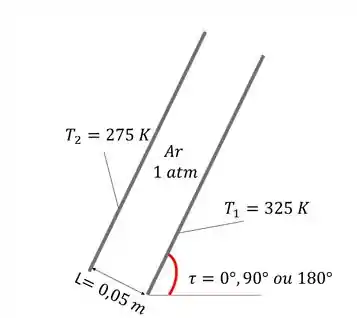
Para resolver essa questão, devemos fluxo de calor por convecção para os três ângulos diferentes, de acordo com a equação abaixo:
Para cada um desses ângulos, nós vamos ter uma forma diferente de calcular os coeficientes de convecção médio, todas elas baseadas num cálculo do número de Nusselt específico para cada aplicação. Isso aí a gente vai discutir nos próximos passos :)
Antes de ir nos próximos passos, a gente tem que aprender a calcular o número de Rayleigh para uma placa plana:
Sendo o espaço entre as placas, a aceleração da gravidade, o coeficiente de expansão térmica do ar, a viscosidade cinemática do ar e a difusividade térmica do ar.
Pra resolver a questão vamo precisar buscar as propriedades do ar a 1 atm na Tabela A.4 (página 634) a uma temperatura média entre de :
Pronto, agora podemos resolver a questão nos próximos passos.
Passo 2
Em primeiro lugar, vamos calcular o número de Nusselt para a posição vertical, ou seja, .
Temos que começar calculando o número de Rayleigh:
Para calcular o número de Nusselt, vamos utilizar a expressão para convecção natural entre placas verticais:
Pra finalizar esse passo, vamos calcular o fluxo térmico para :
Passo 3
Vamos analisar a situação em que , onde temos cavidade horizontal com aquecimento na superfície inferior, no qual o número de Nusselt pode ser calculado a partir da correlação de Globe e Dropkin:
Agora, vamos calcular o fluxo térmico para :
Passo 4
Já para , temos uma cavidade horizontal com aquecimento na superfície superior.
Para esse caso, é beeeem mais fácil calcular o número de Nusselt. Por definição, temos que o número de Nusselt é basicamente 1, pois não há convecção natural. O que acontece aqui é que como o ar quente (menos denso) já tá em cima, não tem como criar correntes de convecção, e temos transferência de calor basicamente por condução.
Pra finaliza a questão, vamos calcular o fluxo térmico para :
Pronto, matamos essa questão juntos!
Resposta
Os fluxos térmicos pra cada uma das três situações, são: , e .