Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 9.Problemas - Ex. 113

Um tubo horizontal com 100   m m de diâmetro transporta óleo quente que deve ser usado no projeto de um aquecedor de água industrial. Com base em uma vazão consumida de água típica, sua velocidade sobre o tubo é de 0,5   m / s . O óleo quente mantém a temperatura da superfície externa do tubo a 85 ° C e a temperatura da água é de 37 ° C .

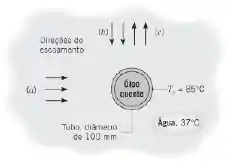
Investigue o efeito da direção do escoamento sobre a taxa de transferência de calor ( W / m ) para escoamentos: (a) horizontal, (b) descendente e (c) ascendente.

Passo 1

Começamos o problema calculando a temperatura de filme:

T f = T s + T ∞ 2

Sendo:

T s = 85 ° C ;

T ∞ = 37 ° C .

Temos:

T f = 85 + 37 2

T f = 61 ° C = 334   K ≅ 335   K

Pela Tabela A .   4 obtemos as seguintes propriedades da água sob a temperatura de filme:

ρ f = 982,3   k g / m 3

μ f = 453 × 10 - 6   N ⋅ s / m 2

v = μ f ρ f = 4,625 × 10 - 7 m 2 / s

k = 0,656   W / m ⋅ K

v f = 1,018 × 10 - 3   m 3 / k g

c p = 4186   J / k g ⋅ K

α = 1,595 × 10 - 7   m 2 / s

β = 535,5 × 10 - 6   K - 1

P r = 2,88

Passo 2

Letra a)

H o r i z o n t a l

Calculando R a D :

R a D = g β T s - T ∞ D 3 v α

Dados:

g = 9,8   m / s 2 ;

D = 100   m m = 0,1   m .

Temos:

R a D = 9,8 ⋅ 535,5 × 10 - 6 ⋅ 85 - 37 ⋅ 0,1 3 4,625 × 10 - 7 ⋅ ( 1,595 × 10 - 7 )

R a D = 3,43 × 10 9

R a D ≥ 10 9   ,   o   f l u x o   é   t u r b u l e n t o

O critério para determinar se a convecção livre ou forçada está dominando nas condições operacionais do fluxo é a razão:

G r D R e D 2

Calculando G r D :

R a D = G r D P r

Para a água ( T f = 335   K ):

P r = 2,88 .

Temos:

3,43 × 10 9 = G r D ⋅ 2,88

G r D = 1,2 × 10 9

Calculando R e D :

R e D = V D v

Para a água  ( T ∞ = 310   K ):

A viscosidade da água:

v = μ f ρ f

Sendo:

ρ f = 993   k g / m 3 ;

μ f = 695 × 10 - 6   N ⋅ s / m 2 .

Temos:

v = 695 × 10 - 6 993

v = 6,99 × 10 - 7   m 2 / s

Desse modo, com V = 0,5   m / s :

R e D = 0,5 ⋅ 0,1 6,99 × 10 - 7

R e D = 7,15 × 10 4

Voltando:

G r D R e D 2 = 1,2 × 10 9 7,15 × 10 4 2

G r D R e D 2 = 0,23 < 1

O regime de convecção mista está presente.

Passo 3

A correlação para transferência de calor por convecção mista para fluxos externos e internos é expressa por:

N u ¯ n = N u ¯ F n ± N u ¯ N n

Com n = 4  para geometria de um tubo horizontal.

N u ¯ 4 = N u ¯ F 4 ± N u ¯ N 4

Como R a D ≤ 10 12 ·, o número de Nusselt de Churchill e a correlação são expressas como:

N u ¯ N = 0,60 + 0,389 R a D 1 6 1 + 0,559 P r 9 16 8 27 2

Substituindo os termos:

N u ¯ N = 0,60 + 0,389 ⋅ 3,43 × 10 9 1 6 1 + 0,559 2,88 9 16 8 27 2

N u ¯ N = 20 1,9

O número de Nusselt determinado a partir da correlação da convecção forçada é expresso como:

N u ¯ F = 0,26 R e D 0,6 P r 0,37 P r P r s 0,25

Para a água ( T ∞ = 310   K ) :

P r = 4,62

Para a água ( T s = 358   K ) :

P r s = 2,07

Substituindo os termos:

N u ¯ F = 0,26 ⋅ 7,15 × 10 4 0,6 ⋅ 4,62 0,37 4,62 2,07 0,25

N u ¯ F = 457,65

Substituindo N u ¯ N e N u ¯ F na correlação apresentada anteriormente:

N u ¯ 4 = 457,65 4 + 201,9 4

N u ¯ = 461,9

Passo 4

O número de Nusselt pode ser expresso como:

N u ¯ = h ¯ L k = 461,9

Substituindo os termos:

461,9 = h ¯ ⋅ 0,1 0,656

h ¯ = 3030   W / m 2 ⋅ K

A equação do fluxo térmico se dá:

q ' = h ¯ A s T s - T ∞

q ' = h ¯ π L T s - T ∞

Assim:

q ' = 3030 ⋅ π ⋅ 0,1 ⋅ 85 - 37

q ' = 45,69   k W / m

Passo 5

Letra b)

D e s c e n d e n t e

Voltando na correlação para transferência de calor por convecção mista para fluxos externos e internos: N u ¯ n = N u ¯ F n ± N u ¯ N n

Com n = 3  para geometria de um tubo horizontal com fluxo oposto:

N u ¯ 3 = N u ¯ F 3 - N u ¯ N 3

Substituindo N u ¯ N e N u ¯ F na correlação apresentada anteriormente:

N u ¯ 3 = 457,65 3 - 201,9 3

N u ¯ = 444,15

O número de Nusselt pode ser expresso como:

N u ¯ = h ¯ L k = 444,15

Substituindo os termos:

444,15 = h ¯ ⋅ 0,1 0,656

h ¯ = 2913,62   W / m 2 ⋅ K

A equação do fluxo térmico se dá:

q ' = h ¯ A s T s - T ∞

q ' = h ¯ π L T s - T ∞

Assim:

q ' = 2913,62 ⋅ π ⋅ 0,1 ⋅ 85 - 37

q ' = 43,94   k W / m

Passo 6

Letra c)

A s c e n d e n t e

Voltando na correlação para transferência de calor por convecção mista para fluxos externos e internos: N u ¯ n = N u ¯ F n ± N u ¯ N n

Com n = 3  para geometria de um tubo horizontal com fluxo auxiliar:

N u ¯ 3 = N u ¯ F 3 + N u ¯ N 3

Substituindo N u ¯ N e N u ¯ F na correlação apresentada anteriormente:

N u ¯ 3 = 457,65 3 + 201,9 3

N u ¯ = 470,4

O número de Nusselt pode ser expresso como:

N u ¯ = h ¯ L k = 470,4

Substituindo os termos:

470,4 = h ¯ ⋅ 0,1 0,656

h ¯ = 3085,6   W / m 2 ⋅ K

A equação do fluxo térmico se dá:

q ' = h ¯ A s T s - T ∞

q ' = h ¯ π L T s - T ∞

Assim:

q ' = 3085,6 ⋅ π ⋅ 0,1 ⋅ 85 - 37

q ' = 46,53   k W / m

Resposta

a )   q ' = 45,69   k W / m

b )   q ' = 43,94   k W / m

c )  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um bloco de gelo seco esférico a -79°C é exposto ao ar atmosférico a 30°C. A direção geral em que o ar se move na presente situação é (a) horizontal(b) para cima(c) para baixo(d) recirculação ao redor
Considere um ovo cozido quente em uma nave espacial preenchida com ar à pressão e temperatura atmosféricas o tempo todo. Desconsiderando qualquer efeito da radiação, o ovo resfriará mais rapidamente o
Considere um cilindro horizontal de 0,2 m de diâmetro e 1,8 m de comprimento em uma sala a 20°C. Considerando que a temperatura da superfície externa do cilindro é 40°C, o coeficiente de transferência
Calcule o coeficiente convectivo médio natural de transferência de massa para uma esfera de naftaleno de 3c m de diâmetro, mantida em um ambiente a 60° Ce 1 a t m .
Na extração de óleo da pimenta-do-reino em um leito fixo, cuja fração de vazios é de 0,24 , utilizando-se C O 2 supercrítico, Ferreira ( 1996 ) obteve-se os seguintes resultados:(a) Verifique qual é o