Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas - Ex. 148

Um tubo liso contém etanol a 20°C escoando a 7 m³/h por uma obstrução de Bernoulli, como na figura abaixo. São instalados três tubos piezométricos, como mostrado também. Se a obstrução é uma placa de orifício, calcule os níveis piezométricos (a) h2 e (b) h3.

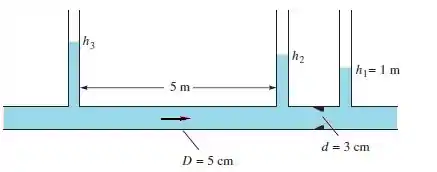
Passo 1

E ai, galera! Tranquilidade? Bora que bora encarar mais um desafio?

Vamos pegar as propriedades do etanol a 20°C!!

ρ = 789 k g m 3

μ = 0,0012 k g m . s

Com a vazão a gente consegue calcular Reynold e como é um tubo liso, podemos obter o valor do fator de atrito no diagrama de Moody rs!

R e = 4 Q ρ π D μ = 4 7 3600 789 π 0,05 0,0012 = 32600

No diagrama de Moody, esse Reynold na curva de tubo liso nos concederá um valor de

f = 0,023

Passo 2

Bem, se a gente calcular qual é o β desse sistema, teremos que:

β = d D = 3 5 = 0,6

Vamos dar uma olhadinha nesse gráfico aqui ó:

A gente observa que para β = 0,6 para uma placa plana, o valor de K = 1,5 aproximadamente.

Passo 3

(a) Portanto, a perda de carga através do orifício é:

Δ h = h 2 - h 1 = K V t 2 2 g

V t = Q A = 7 3600 π 4 0,05 2 = 0,99   m / s

Δ h = 1,5 0,99 0,6 2 2 2 9,81 = 0,58   m

Logo, h 2 = h 1 + 0,58 = 1 + 0,58 = 1,58   m

Passo 4

(b) Também temos que a diferença de alturas h 3 - h 2 é devido a perda de carga, porém como não se trata de um orifício, a gente pode calcular essa perda de carga da forma clássica por Bernoulli!

Δ h = h 3 - h 2 = f L D V 2 2 g = 0,023 5 0,05 0,99 2 2 9,81 = 0,12   m

h 3 = 1,58 + 0,12 = 1,7   m

Resposta

a h 2 = 1,58   m

b h 3 = 1,7   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o escoamento de água a 20°C na figura abaixo, use a combinação de tubo de Pitot e tomada de pressão estática para calcular (a) a velocidade na linha de centro e (b) a vazão volumétrica no tubo li
Uma solução precisa do problema P6.143, usando a figura abaixo, requer iteração porque tanto a ordenada como a abcissa dessa figura contêm a vazão Q, que é incógnita. No espírito do exemplo 5.11, enco
Um pesquisador precisa medir a velocidade do escoamento momento em um túnel de água. Devido às restrições orçamentárias, ele não dispõe de um tubo de Pitot estático, mas, em vez disso, insere uma sond
Um engenheiro que curso mecânica dos fluidos na faculdade sem fundamentos sólidos colocou uma tomada de pressão estática a montante e longe da sonda de estagnação, como mostra na figura abaixo, compro