Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas - Ex. 147

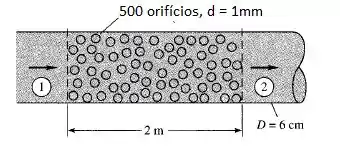
Ar escoa por um tubo liso de 6 cm de diâmetro que tem uma seção perfurada de 2 m de comprimento contentando 500 furos (diâmetro de 1 mm), como na figura abaixo. A pressão externa ao tubo é a pressão padrão ao nível do mar. Se p 1 = 105   k P a e Q 1 = 110   m 3 / h , calcule p 2 e Q 2 , considerando os furos como se fossem aproximados por placas de orifício. Dica: Um volume de controle para quantidade de movimento pode ser muito útil.

Passo 1

E ai, galera! Tranquilidade? Bora que bora encarar mais um desafio?

Vamos tomar as propriedades do ar em 20°C e 105 kPa!!!

ρ = 1,25 k g m 3

μ = 1,8   x   10 - 5 k g m . s

Bem, usando a vazão de entrada a gente consegue ter uma estimativa de qual é a velocidade no ponto 1, certo?

V 1 = Q 1 A = 110 3600 π 4 0,06 2 = 10 ,   8 m s

R e 1 = ρ V 1 D μ = 1,25 10,8 0,06 1,8   x   10 - 5 = 45000

Bem, esse cara é um tubo liso de acordo com o nosso enunciado, ou seja, se eu tenho Reynold e sei que é um tubo liso, basta ir no diagrama de Moody e obtermos o fator de atrito :D

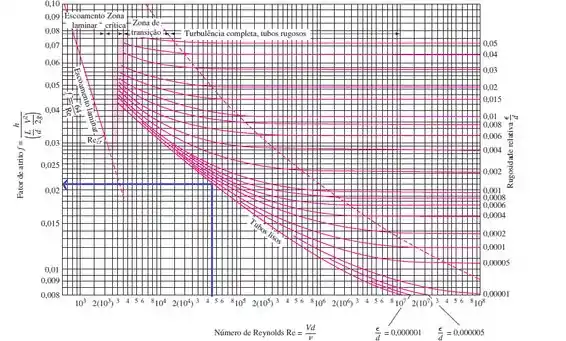
Opa, temos um valor de aproximadamente f = 0,0214

Passo 2

Portanto, a gente tem que a tensão de cisalhamento na parede pode ser dada por:

τ p = f 8   ρ V 2 = 0,0214 8 1,25 10,8 2 = 0,390   P a

Bem, a gente quer calcular a vazão né? Então vamos usar a equação que relaciona orifícios com isso!!

Q = C d A t 2 Δ p ρ 1 - β 4

Passo 3

Vamos agora assumir duas coisas importantes aqui:

A primeira é dizer que β → 0 porque temos que os diâmetros dos orifícios são muitoooo menores do que o diâmetro do tubo! Quando isso acontece, um valor bem típico de C d = 0,61 ou C d = 0,6 é dado! Então fica aí mais uma dica!! Quando β → 0 , esses são os valores mais típicos para CD.

Segunda coisa importante é que vamos assumir que não há uma queda de pressão tão absurda, então Δ p o r i f í c i o = 105000 - 101350 = 3650   P a

Q = N o r i f í c i o s C d A t 2 Δ p ρ 1 - β 4

Q = 500 0,61 π 4 0,001 2 2 3650 1,25 1 2 = 0,0183   m 3 / s

Então

Q 2 = Q 1 - 0,0183 ≈ 110 3600 - 0,0183 = 0,01225   m 3 / s

Passo 4

Portanto

V 2 = Q 2 A = 0,01225 π 4 0,06 2 = 4,33   m / s

Se fizermos um volume de controle em volta do nosso tubo, temos o seguinte balanço de forças na direção x:

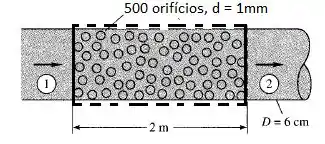
∑ F x = p 1 A - p 2 A - τ p π D L = m ˙ 2 V 2 - m ˙ 1 V 1 = ρ A V 1 2 - ρ A V 2 2

Dividindo toda nossa equação pela área, temos ao final:

p 1 - p 2 = 0,390 π 0,06 2 π 4 0,06 2 + 1,25 4,33 2 - 1,25 10,8 2 = 52 + 23 - 146 = - 71 P a

p 2 = 105000 + 71 = 105   k P a

Note que esse valor encontrado foi o que assumimos inicialmente, o que indica que a vazão Q 2 = 0,0125   m 3 / s é uma vazão bem próxima da real!

Resposta

Q 2 = 0,0125   m 3 / s

p 2 = 105   k P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Querosene a 20°C escoa a 20 m³/h em um tubo de 8 cm de diâmetro. O escoamento deve ser medido por meio de um bocal ISA 1932 de modo que a queda de pressão seja 7kPa. Qual é o diâmetro apropriado do bo
Ar escoa a alta velocidade por um medidor venturi Herchel monitorado por um manômetro de mercúrio, conforme mostrado abaixo. As condições a montante são 150 kPa e 80°C. Se h = 37 cm, estime a vazão em
Deseja-se medir um escoamento de gasolina a 20°C em um tubo de 12 cm de diâmetro, usando um bocal Venturi moderno. Para que os padrões internacionais sejam válidos (figura 6.43), qual é a gama admissí
Um bocal venturi moderno é calibrado em um escoamento de laboratório com água a 20°C. O diâmetro do tubo é 5,5 cm, e o diâmetro da garganta do venturi é 3,5 cm. A vazão é medida por meio de um tanque
Dois reservatórios contendo água, cada qual com área da base de 929 m², estão conectados por um bocal de raio longo de 13 mm de diâmetro, como na figura abaixo. Se h = 30,5 cm , como mostrado para t =