Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 10.Problemas - Ex. 50
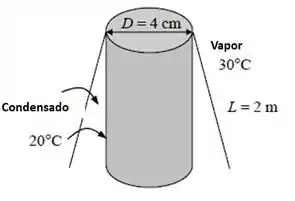
Vapor saturado a 30°C condensa na parte externa de um tubo vertical de 4 cm de diâmetro externo e 2 m de comprimento. A temperatura do tubo é mantida 20°C pela água de resfriamento. Determine (a) a taxa de transferência de calor do vapor para a água de resfriamento, (b) a taxa de condensação do vapor de água e (c) a espessura aproximada da película de líquido na parte de baixo do tubo.
Passo 1
Como sempre, nossos primeiro passo é catar as propriedades do vapor saturado e do condensado na temperatura de filme, beleza?
Nesses problemas de condensação/vaporização, a gente sempre tem que catar o calor latente na temperatura de saturação do fluido. Nesse caso como é água, temos Tsat = 30°C
Passo 2
(a) Como não temos ainda como calcular Reynold da forma usual porque não temos nenhuma informação sobre velocidade ou vazão. Então gente vai assumir que o escoamento de condensação seja laminar e é muito comum fazermos isso para esse tipo de escoamento, e usar uma fórmula alternativa para calcular Reynold nesse tipo de problema.
Vamos calcular hfg’ depois Reynold e em seguida h!!!
Novamente, vamos ter que substituir os valores de cada variável SEMPRE PRESTANDO ATENÇÃO NOS ÍNDICES DE CADA VARIÁVEL, ok?
Fazendo isso a gente vai encontrar o valor de , o que indica que foi uma boa consideração que fizemos ao dizer que tem escoamento laminar
Passo 3
Seguimos aqui calculando o coeficiente convectivo da seguinte forma:
Portanto,
Passo 4
(b) Aqui é só a gente igualar a quantidade de calor trocada com a equação associada a condensação !!!
Passo 5
(c) Parece que é assustador calcular essa espessura, né? Mas não é!!! Você só precisa se lembrar de duas equações pequenas
Agora a gente só isola hl na segunda equação e joga na primeira e daí é só continha :D