Um vaso muito alto com de diâmetro contém de água. Quando sua rotação é aumentada uniformemente para atingir a rotação de corpo rígido, aparece uma área seca de de diâmetro no fundo do vaso. Qual é a rotação em para essa condição?
Passo 1
Fala galera!! Bora resolver essa questão comigo!!
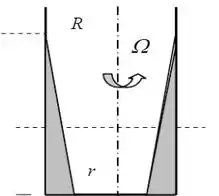
Queremos aqui, encontrar a rotação em para a condição especificada no problema. Podemos fazer a seguinte representação do processo:
Passo 2
Uma maneira de resolver essa questão é pelo cálculo do volume do liquido formado pela rotação do vaso. Como não a perda de liquido, esse volume será o inicial. Assim, temos que o volume do líquido sombreado no esquema acima em termos do raio do vaso e do raio no ponto seco formado pela rotação é:
Temos que pode ser obtido a partir da relação:
Diferenciando, temos:
Substituindo na equação do volume, teremos o seguinte:
Integrando de até , temos o seguinte:
Substituindo os valores, temos:
Transformando em , temos:
Portanto, a rotação necessária é .