Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas - Ex. 150
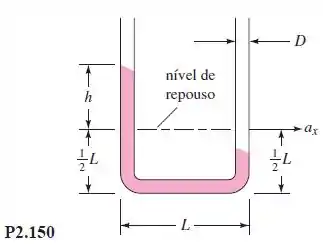
Um acelerômetro barato, que provavelmente vale pelo que custa, pode ser feito com um tubo em , como na Figura P2.150. Se e , qual será a altura se ? As marcações da escala sobre o tubo podem ser múltiplos lineares de ?
Passo 1
Fala Galera!! Vem comigo resolver essa questão!!
Nesse problema, nós queremos a altura que será formado quando sofre uma aceleração de . Se assumimos que o diâmetro é tão pequeno, , que a superfície livre é um "ponto". Então a seguinte equação se aplica:
Passo 2
Como a tangente de um angulo pode ser dado pelo cateto oposto divido pelo cateto adjacente, por relação trigonométrica, podemos dizer que:
Substituindo, temos:
Uma vez que , as leituras da escala são de fato lineares em , mas eu não o recomendo como um acelerômetro real, há muitas imprecisões e desvantagens.
Resposta
São lineares