Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas - Ex. 155

Para que rotação uniforme em rpm em torno do eixo C o tubo em U da Figura P2.155 assumirá a configuração mostrada? O fluido é o mercúrio a 20 ℃ .

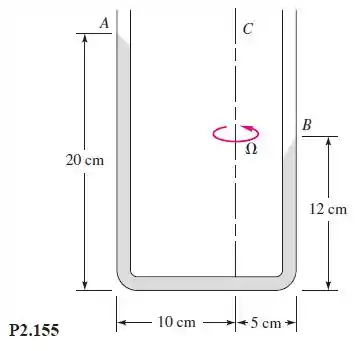
Passo 1

Fala Galera!! Vem comigo resolver mais uma questão!!

Nesse problema, nós queremos encontrar a rotação em r p m em torno do eixo C para que o liquido no tubo assuma a configuração mostrada na figura do problema.

Passo 2

Para começar, podemos definir h 0 a altura da superfície livre na linha central. Então, a rotação necessária pode ser dada por:

z B = h 0 + Ω 2 R B 2 2 g

E

z A = h 0 + Ω 2 R A 2 2 g

Subtraindo, temos:

z A - z B = h 0 + Ω 2 R A 2 2 g - h 0 + Ω 2 R B 2 2 g

z A - z B = Ω 2 2 g R A 2 - R B 2

Para R B = 0,05   m , R A = 0,1   m , z A = 0,2   m , z B = 0,12   m e g = 9,81   m / s 2 temos o seguinte:

0,2   - 0,12 = Ω 2 2 9,81 0,1 2 - 0,05 2

Ω 2 = 209,28

Ω = 14,47   r a d / s

Transformando em r p m , temos:

Ω = 14,47   r a d / s 60   s 1   m i n 1   r e v 2 π   r a d

Ω = 138   r p m

Portanto, é necessária uma rotação de 138   r p m .

Resposta

Ω = 138   r p m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O tanque de água da Figura P2.143 está cheio e aberto para a atmosfera no ponto A . Para qual aceleração a x em m / s 2 a pressão no ponto B será (a) a atmosférica e (b) o zero absoluto?
O tanque de líquido da Figura P2.139 acelera para a direita com o fluido em movimento de corpo rígido. (a) Calcule a x em m / s 2 . (b) Por que a solução da parte (a) não depende da massa específica d
Uma criança está segurando um fio que está atado a um balão cheio de hélio. (a) A criança está parada em pé e subitamente acelera para a frente. Em um sistema de referência movendo-se juntamente com a
O manômetro de três ramos da Figura P2.159 é preenchido com água até uma profundidade de 20c m . Todos os tubos são longos e têm diâmetros pequenos. Se o sistema gira a uma velocidade angular Ω em tor
O tanque de água na Figura P2.147 acelera uniformemente descendo livremente um declive de 30 ° . Se as rodas não tiverem atrito, qual é o ângulo θ ? Você pode explicar esse interessante resultado?