A velocidade terminal, , de caixas de transporte deslizando para baixo sobre uma camada de ar em uma rampa (injetada por meio de inúmeros orifícios na superfície inclinada) depende da massa da caixa, , da área da base, , da aceleração da gravidade, , do ângulo de inclinação da rampa, , da viscosidade do ar, , e da espessura da camada de ar, . Use a análise dimensional para encontrar os parâmetros que caracterizam este fenômeno.
Passo 1
Fala aiii, tudo bem? Nessa questão nos é dito que a velocidade depende da massa, área, gravidade, inclinação e viscosidade e espessura do ar e, usando a análise dimensional, vamos encontrar os parâmetros , para isso vamos usar o Excel, beleza? Então bora lá!
Passo 2
Repara que nós temos que,
O número de parâmetros é:
O número de dimensões primárias é:
O número de parâmetros de repetição é:
Show? Então o número de grupos é:
Passo 3
Agora podemos partir para o Excel!
Vamos inserir as dimensões dos parâmetros de repetição e de até quatro outros parâmetros (para até quatro grupos ). A planilha calculará os expoentes a, b e c para cada um.
Repetindo os parâmetros escolhendo e , temos:
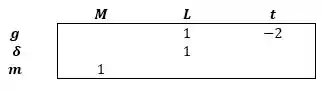
Passo 4
Fazendo agora os grupos , temos que o primeiro grupo vai ser:
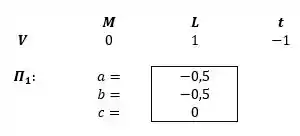
Para o segundo grupo:
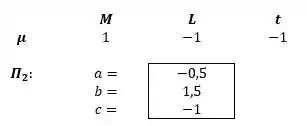
Para o terceiro grupo:
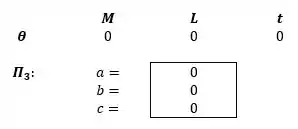
E por fim, para o quarto grupo:
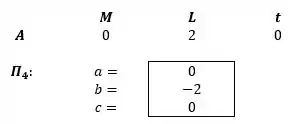
Passo 5
A partir dos grupos acima temos que:
Observe que os grupos ,e podem ser obtidos por inspeção.