A ventilação na boate de um navio de turismo é insuficiente para limpar a fumaça de cigarros e similares (neste navio ainda não é completamente proibido fumar). Testes devem ser realizados para verificar se um ventilador extrator mais potente funcionará. A concentração de fumaça, (partículas por metro cúbico de ar), depende do número de fumantes, , da perda de pressão produzida pelo ventilador, , do diâmetro do ventilador, , da velocidade do motor, , da massa específica das partículas de fumaça e do ar, e , respectivamente, da aceleração da gravidade, , e da viscosidade do ar, . Determine os parâmetros adimensionais que caracterizam este problema.

Usando o procedimento de Buckingham temos que o número de parâmetros é:

Selecionando as dimensões primárias

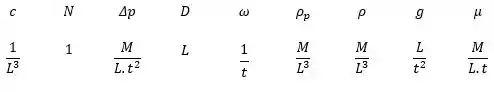
E os parâmetros repetidos:

Então nós temos grupos sem dimensão. Configurando as seguintes equações dimensionais:

Somando os expoentes:

Temos que a solução do sistema é:

Então:

Para o segundo grupo temos:

Somando os expoentes:

Temos que a solução do sistema é:

Então:

Os outros grupos podem ser encontrados por inspeção:

Verifcando usando como dimensões primárias temos: