Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 11.Problemas - Ex. 1
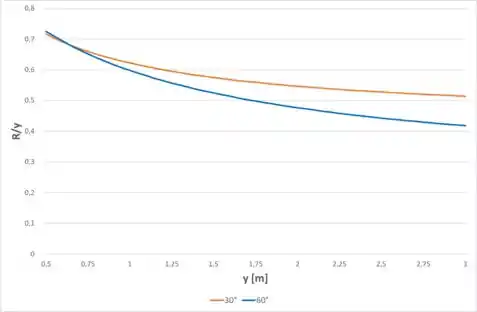
Verifique a equação dada na Tabela 11.1 para o raio hidráulico de um canal trapezoidal. Trace o gráfico da taxa para com inclinações do lado de 30° e 60° para .
Passo 1
Tá legal! O canal trapezoidal é dado por:
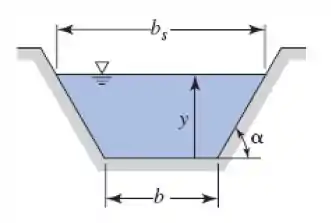
Então vamos começar encontrando a equação para a área do canal, que pode ser encontrada dividindo a área em dois triângulos e um retângulo, e dessa forma, temos:
E, colocando em evidência, temos:
Que é a mesma equação fornecida na tabela 11.1
Passo 2
Agora, vamos encontrar o perímetro molhado, que é o comprimento em contato com o fluído, então, temos a parcela inferior do retângulo e as duas parcelas laterais dos triângulos, dessa forma:
Que é a mesma fórmula fornecida na tabela 11.1.
Passo 3
Agora, para encontrar uma relação para o raio hidráulico, devemos fazer:
Substituindo os valores conhecidos, temos:
E, estamos no caminho certo, pois essa é a equação fornecida na tabela 11.1.
Passo 4
Agora, para plotar o gráfico de devemos dividir a equação de encontrada no passo 3 por , então, temos:
Então, para , e e , temos:
