Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 12.Problemas - Ex. 1
Um avião de alta velocidade cruza o ar. Como a temperatura do ar no nariz do avião difere da temperatura do ar que está a uma certa distância do avião?
Passo 1
Bom pessoal, essa questão é um problema de estagnação! Lembra quando falamos da sonda de Pitot?
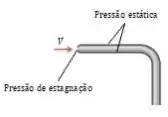
Em que próximo do orifício, medimos a pressão de estagnação, a qual é maior já que todo fluido começa a “brigar” para passar de um lado ao outro?? Então!!
Da mesma forma acontece com a temperatura do ar no nariz do avião, em escoamentos com alta velocidade a temperatura medida por uma sonda estacionária colocada no fluido (temperatura de estagnação) pode ser significativamente mais alta do que a temperatura estática do fluido.
Passo 2
Vamos ver isso melhor, a temperatura durante um processo é chamada de temperatura dinâmica:
Quando o ar é levado a ponta da sonda, temos temperatura de estagnação:
Que é temperatura estática +dinâmica, por isso é mais alta!
Certinho??
Resposta
Em escoamentos com alta velocidade a temperatura medida por uma sonda estacionária colocada no fluido (temperatura de estagnação) pode ser significativamente mais alta do que a temperatura estática do fluido.