Enunciado
Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 34.Problemas Desafiadores - Ex. 115
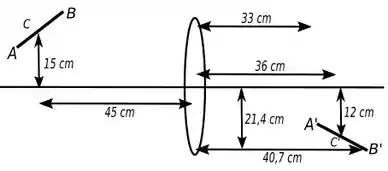
115. Um objeto inclinado. Um lápis com de comprimento é colocado formando um ângulo de com a horizontal e seu centro está situado a acima do eixo ótico e a de uma lente com distância focal igual a , como indica a Figura . (Note que a figura não foi desenhada em escala.) Suponha que o diâmetro da lente seja suficientemente grande para que a aproximação de raios paraxiais seja válida. Onde
está a imagem do lápis? (Indique o local onde se formam as imagens dos pontos objetos e localizados, respectivamente, na extremidade da borracha, na ponta e no centro do lápis.) Qual é o comprimento da imagem? (Ou seja, qual é a distância entre as imagens dos pontos e ?) Faça um desenho esquemático para mostrar a orientação da imagem.
Passo 1
Então galera, olá novamente!
Vamos começar a queimar neurônios, para responder o que o item quer vamos fazer como ele mesmo sugeriu que é achar as posições (altura e distância da lente) de , e .
Para encontrar a distância de cada ponto da lente, podemos usar a seguinte equação:
Onde teremos que achar .
E para encontrar a altura de cada ponto podemos usar uma semelhança de triângulos entre as alturas e as distancias entre os pontos e as lentes assim:
Para encontrar o comprimento da imagem podemos usar a fórmula de distância entre pontos onde a distância entre a lente e o ponto é a coordenada e altura do ponto a coordenada , assim:
Depois disso tudo poderemos fazer nosso desenho pedido em .
Vamos achar as posições de cada ponto em passos diferentes.
Passo 2
Vamos começar com o ponto .
Primeiro vamos encontrar , temos:
Temos que é dado por , assim temos que:
Agora vamos encontrar , temos o seguinte:
Onde temos que é dado por , assim temos que:
Passo 3
Agora vamos para o ponto .
Primeiro vamos encontrar , temos:
Temos que é dado por , assim temos que:
Agora vamos encontrar , temos o seguinte:
Onde temos que é dado por , assim temos que:
Passo 4
Agora vamos para o ponto .
Primeiro vamos encontrar , temos:
Temos que vale , assim temos que:
Agora vamos encontrar , temos o seguinte:
Onde temos que vale , assim temos que:
Passo 5
Agora vamos encontrar o comprimento da imagem da forma como falei no passo um , temos:
Substituindo o que sabemos, temos:
Então temos que:
Passo 6
Agora vamos para o desenho esquemático, ele fica da seguinte forma:
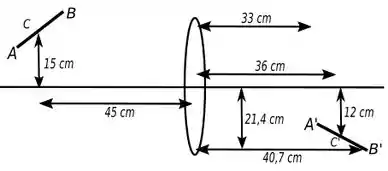
Resposta
